Skip over navigation
It is helpful to find what these two triangles have in common. Angle PQR (or SQR), shown in red on the right, is an angle in both triangles.
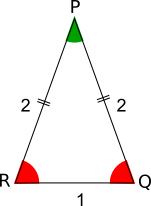
Triangle PQR is isosceles, so angle PRQ is equal to angle PQR. It is also shown in red in the diagram on the left.
The green angle at P is the angle that needs to be added to two red angles to make 180$^\circ$.
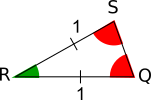Triangle QRS is also isosceles, and its line of symmetry is through R. So angle RSQ is equal to angle SQR. It is also shown in red in the diagram on the right.
The angle at R also makes a sum of 180$^\circ$ when added to the two red angles. So it is equal to the green angle at P.
But this means that the triangles PQR and QRS are similar.
We can use either that the scale factor between triangle QRS and triangle PQR is 2 (shown below in the diagram on the left), or that the ratio between the longer sides and the shorter side of each triangle is 1:2 (shown below in the diagram on the right).
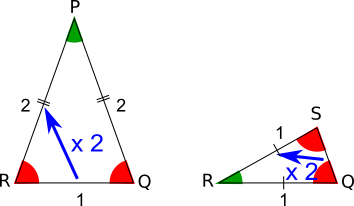
Either of these facts about similar triangles tell us that QS = $\frac12$.
Doubly Isosceles
Age 14 to 16
ShortChallenge Level 
It is helpful to find what these two triangles have in common. Angle PQR (or SQR), shown in red on the right, is an angle in both triangles.
Triangle PQR is isosceles, so angle PRQ is equal to angle PQR. It is also shown in red in the diagram on the left.
The green angle at P is the angle that needs to be added to two red angles to make 180$^\circ$.
Triangle QRS is also isosceles, and its line of symmetry is through R. So angle RSQ is equal to angle SQR. It is also shown in red in the diagram on the right.The angle at R also makes a sum of 180$^\circ$ when added to the two red angles. So it is equal to the green angle at P.
But this means that the triangles PQR and QRS are similar.
We can use either that the scale factor between triangle QRS and triangle PQR is 2 (shown below in the diagram on the left), or that the ratio between the longer sides and the shorter side of each triangle is 1:2 (shown below in the diagram on the right).
Either of these facts about similar triangles tell us that QS = $\frac12$.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Fitting In
The largest square which fits into a circle is ABCD and EFGH is a square with G and H on the line CD and E and F on the circumference of the circle. Show that AB = 5EF. Similarly the largest equilateral triangle which fits into a circle is LMN and PQR is an equilateral triangle with P and Q on the line LM and R on the circumference of the circle. Show that LM = 3PQ
Triangle Midpoints
You are only given the three midpoints of the sides of a triangle. How can you construct the original triangle?