Skip over navigation
Probability of getting a white marble:
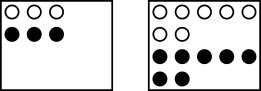
If half the marbles in each box are white,
the probability that she wins her freedom is $\frac12$
Otherwise, one box will be more than $\frac12$ white and the other will be less than $\frac12$ white.
To maximise her probability of freedom we need to get as close to $1$ in one box and to $\frac12$ in the other box as possible. We do this by putting just one white marble in one box:
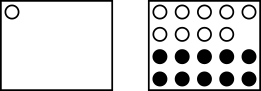
Probability of freedom is $\frac12\times(1+\frac9{19})=\frac{28}{38}$, which is nearly $74\%$.
Winning Marble
Age 14 to 16
ShortChallenge Level 
Probability of getting a white marble:
$\frac12\times(${proportion white in box 1} $+$ {proportion white in box 2}$)$
If half the marbles in each box are white,
the probability that she wins her freedom is $\frac12$
Otherwise, one box will be more than $\frac12$ white and the other will be less than $\frac12$ white.
To maximise her probability of freedom we need to get as close to $1$ in one box and to $\frac12$ in the other box as possible. We do this by putting just one white marble in one box:
Probability of freedom is $\frac12\times(1+\frac9{19})=\frac{28}{38}$, which is nearly $74\%$.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
In a Box
Chris and Jo put two red and four blue ribbons in a box. They each pick a ribbon from the box without looking. Jo wins if the two ribbons are the same colour. Is the game fair?
Chances Are
Which of these games would you play to give yourself the best possible chance of winning a prize?
