Square Surprise

Yousef from Emirates International School in Egypt wrote:

In order to solve this, you have to consider all options of where the blue dot will go. A way to do this is by removing all the red dots then considering the spaces where the blue one could be then replacing the red dots again.
So in the end, it seems that the dot will have to go in one space.

Majid from Essex Primary sent in this:

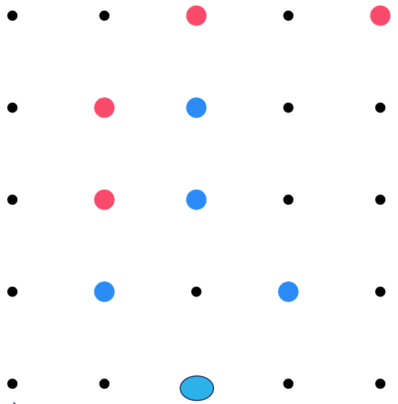 If I were the blue player, I would put it anywhere as the pink does not have a chance to make a square. When a chance is in sight for the pink, I would put it on the t dot on the bottom row. That would be a square but it would just be orientated, in the shape of a diamond. (It is interesting you refer to a 'diamond'.  Is this shape a square?)
The computer might block you, so to be on the safe side you would put it on the 3rd dot on the bottom row as shown here.






Scout from James Allen's Prep School sent in the following:

When the computer conquers (in red) three corners I must click the fourth corner otherwise the computer could/would make a square.
The computer double traps you when it can (has two sets of three lined up so wherever you click you still lose). To win I would try to double trap the computer.