Skip over navigation
To find out if a sum of three numbers is odd or even, you don't actually need to know the numbers. You only need to know if they are odd or even.
This means that we can replace the numbers on the dice with 'odd' or 'even' (or O and E) without losing any information.
A: 1, 1, 1, 2, 2, 2 becomes O, O, O, E, E, E
B: 3, 3, 4, 4, 5, 5 becomes O, O, E, E, O, O
C: 6, 7, 7, 8, 8, 8 becomes E, O, O, E, E, E
Using a sample space diagram
All possible outcomes can be shown in two tables like the ones below. Two tables are necessary because the outcomes of only two dice can be shown on each table. They can be split only by the outcome on A because it is equally likely to be odd or even.
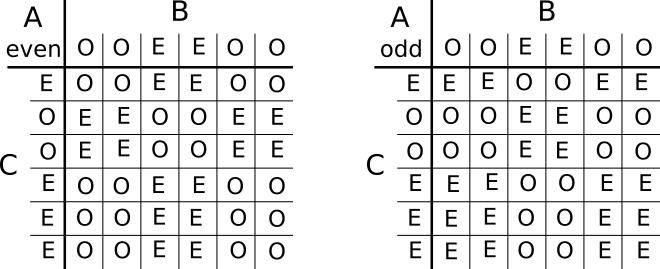
Some of the rows and columns are repeated. A simpler version of the tables is shown below, with fewer rows and columns - but the ratio between the odd and even outcomes on each dice is preserved.
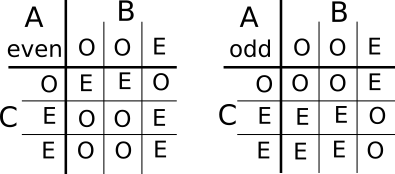
Using the second pair of tables, there are 18 possible outcomes. 9 of them are 'O'. So the probability of getting an odd sum is $\frac12$.
Using a tree diagram
The tree diagram below shows the possible outcomes.
The outcomes where the sum is an odd number are indicated with a green arrow.

So the total probability is: $$\left(\frac12\times\frac23\times\frac13\right)+\left(\frac12\times\frac13\times\frac23\right)+\left(\frac12\times\frac23\times\frac23\right)+\left(\frac12\times\frac13\times\frac13\right)\\
= 2\times\left(\frac12\times\frac23\times\frac13\right)+\left(\frac12\times\frac23\times\frac23\right)+\left(\frac12\times\frac13\times\frac13\right)\\
= 2\times\frac{1\times2\times1}{2\times3\times3}+\frac{1\times2\times2}{2\times3\times3}+\frac{1\times1\times1}{2\times3\times3}\\
=\frac{2\times2}{18}+\frac{4}{18}+\frac{1}{18}\\
=\frac{4+4+1}{18}\\
=\frac9{18}\\
=\frac12$$
Using combinations of products
To add three numbers and get an odd number, the numbers must have all been odd, or two evens and an odd.
The probability that all of the numbers are odd is $\dfrac12\times\dfrac23\times\dfrac13=\dfrac{1}{9}$.
There are three ways of getting two even numbers and an odd number. The odd number could be on any of the three dice.
Die A odd: $\dfrac12\times\dfrac13\times\dfrac23=\dfrac19$
Die B odd: $\dfrac12\times\dfrac23\times\dfrac23=\dfrac29$
Die C odd: $\dfrac12\times\dfrac13\times\dfrac13=\dfrac1{18}$
So the probability of getting an odd sum is: $$\begin{split}\frac19+\frac19+\frac29+\frac1{18}&=\frac2{18}+\frac2{18}+\frac4{18}+\frac1{18}\\&=\frac9{18}=\frac12\end{split}$$


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Odd Dice
Age 14 to 16
ShortChallenge Level 





- Problem
- Solutions
To find out if a sum of three numbers is odd or even, you don't actually need to know the numbers. You only need to know if they are odd or even.
This means that we can replace the numbers on the dice with 'odd' or 'even' (or O and E) without losing any information.
A: 1, 1, 1, 2, 2, 2 becomes O, O, O, E, E, E
B: 3, 3, 4, 4, 5, 5 becomes O, O, E, E, O, O
C: 6, 7, 7, 8, 8, 8 becomes E, O, O, E, E, E
Using a sample space diagram
All possible outcomes can be shown in two tables like the ones below. Two tables are necessary because the outcomes of only two dice can be shown on each table. They can be split only by the outcome on A because it is equally likely to be odd or even.

Some of the rows and columns are repeated. A simpler version of the tables is shown below, with fewer rows and columns - but the ratio between the odd and even outcomes on each dice is preserved.

Using the second pair of tables, there are 18 possible outcomes. 9 of them are 'O'. So the probability of getting an odd sum is $\frac12$.
Using a tree diagram
The tree diagram below shows the possible outcomes.
The outcomes where the sum is an odd number are indicated with a green arrow.

So the total probability is: $$\left(\frac12\times\frac23\times\frac13\right)+\left(\frac12\times\frac13\times\frac23\right)+\left(\frac12\times\frac23\times\frac23\right)+\left(\frac12\times\frac13\times\frac13\right)\\
= 2\times\left(\frac12\times\frac23\times\frac13\right)+\left(\frac12\times\frac23\times\frac23\right)+\left(\frac12\times\frac13\times\frac13\right)\\
= 2\times\frac{1\times2\times1}{2\times3\times3}+\frac{1\times2\times2}{2\times3\times3}+\frac{1\times1\times1}{2\times3\times3}\\
=\frac{2\times2}{18}+\frac{4}{18}+\frac{1}{18}\\
=\frac{4+4+1}{18}\\
=\frac9{18}\\
=\frac12$$
Using combinations of products
To add three numbers and get an odd number, the numbers must have all been odd, or two evens and an odd.
The probability that all of the numbers are odd is $\dfrac12\times\dfrac23\times\dfrac13=\dfrac{1}{9}$.
There are three ways of getting two even numbers and an odd number. The odd number could be on any of the three dice.
Die A odd: $\dfrac12\times\dfrac13\times\dfrac23=\dfrac19$
Die B odd: $\dfrac12\times\dfrac23\times\dfrac23=\dfrac29$
Die C odd: $\dfrac12\times\dfrac13\times\dfrac13=\dfrac1{18}$
So the probability of getting an odd sum is: $$\begin{split}\frac19+\frac19+\frac29+\frac1{18}&=\frac2{18}+\frac2{18}+\frac4{18}+\frac1{18}\\&=\frac9{18}=\frac12\end{split}$$
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
In a Box
Chris and Jo put two red and four blue ribbons in a box. They each pick a ribbon from the box without looking. Jo wins if the two ribbons are the same colour. Is the game fair?
Chances Are
Which of these games would you play to give yourself the best possible chance of winning a prize?

