Skip over navigation
Navjot from Sherborne Qatar answered the questions about the first image in detail. This is Navjot's work:
Assume that its side length is $1$ unit.
Stage 1: 0, no part of the square is blue.
Stage 2: The side of the rotated blue square creates an isosceles right angled triangle with two sides being $0.5$ units (since the blue square's side touches the outer square at its side's midpoint).
So, the length of the blue square's side is: $$\sqrt{0.5^2+0.5^2}=\tfrac{\sqrt2}2$$
Blue area $=\left(\frac{\sqrt2}2\right)^2=\frac24$ of square.
Stage 3: To find the side length of the [purple] square inside the blue square, we can divide $\frac{\sqrt2}2$ by $2,$ [which gives] $\frac{\sqrt2}4$ and use this length to find the side length
by using Pythagoras' Theorem again.
Side length of innermost purple square $=\frac12,$ purple area [of the innermost purple square] $= \left(\frac12\right)^2= \frac14,$ total blue area $= \frac24 -\frac14 = \frac14$ of square.
Stage 4: Side length of innermost blue square $= \frac{\sqrt2}4,$ blue area $=\left(\frac{\sqrt2}4\right)^2=\frac2{16}$ of square.
Stage 5: Side length of innermost purple square $= \frac14,$ purple area $=
\left(\frac14\right)^2 = \frac1{16},$ total blue area $=\frac14 + \left(\frac2{16} - \frac1{16}\right) = \frac14 + \frac1{16}$
If we keep going on we will see that the area of the blue squares keep adding up in the form $\sum{\left(\frac14\right)^n}.$
Being a geometric series with a common ratio $<1,$ the summation will tend to a certain value.
Navjot then used a formula to calculate the sum of the series, and got an answer of $\frac13$. This formula was used by most people who sent in solutions to this problem and can be seen below.
For the next pattern, Alicia from Roedean School used the 'ring' method suggested in the problem. This is Alicia's work:

This shows the outer ring of the pattern. The blue rectangle is twice the area of the pink square, so there is twice as much blue as pink - $\frac13$ of the area is pink and $\frac23$ is blue. The same will be true for each ring added, therefore the overall pattern has twice as much blue as pink.
Sichao from Bangkok Patana School in Thailand found a sequence of fractions and added them up:
 As shown in the diagram the largest section shaded has area of $\frac12$ in respect to the square. The second is exactly $\frac14$ of the first; the third is also exactly $\frac14$ of the second, and so on.
As shown in the diagram the largest section shaded has area of $\frac12$ in respect to the square. The second is exactly $\frac14$ of the first; the third is also exactly $\frac14$ of the second, and so on.
Therefore we know that the areas are:
$\frac 12, \frac18, \frac1{32}, \frac1{128}, ..., \frac1{2\times4^n}$
This [infinite series] we [could write as] $\sum_{n=0}^\infty{\frac1{2\times4^n}}$
To calculate the sum of terms we could rearrange the sum.
Let $S_n$ be the sum of terms.
$S_n=\tfrac12+\tfrac18+\tfrac1{32}+\tfrac1{128}+...$
$\Rightarrow 4S_n=\tfrac 42 +\tfrac48+\tfrac4{32}+\tfrac4{128}+...+\tfrac4{2\times4^n}$
$=2+S_n-\frac2{2\times4^n}$ (by substituting $S_n$)
$\Rightarrow 3S_n=2-\frac2{2\times4^n}$
As $n\rightarrow\infty,$ $\frac2{2\times4^n}\rightarrow0$ because $4^n\rightarrow\infty$
Hence $3S_n=2\Rightarrow S_n=\frac23$
Vignesh from Hymers College in the UK did this in a general case to derive a formula:
We know that the sum of an infinite geometric series is given by the equation:
$S=\frac{a}{1-r}$ (where $a$ is the first term and $r$ is the ratio)
This can be proven:
let, $$S=1+r+r^2....$$
Thus, $$ S\times r=r+r^2+r^3...\\ \Rightarrow S-S\times r=1\\
\Rightarrow S(1-r)=1\\
\Rightarrow S=\tfrac1{1-r}$$
(where $1$ is the first term and $r$ is the ratio)
This can then be applied into each of the patterns.
If the first term is $a$ instead of $1$, then the sequence is $a, ar, ar^2, ...$ and so all of the terms are multiplied by $a$. Multiplying all of the terms by $a$ has the same effect as multiplying the sum by $a$, so the formula is $S=\frac a{1-r}.$
Navjot and Nathan from Sherborne Qatar used this formula more directly. This is Nathan's work for one of the other patterns, including a description of the general strategy:


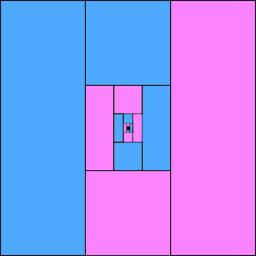

Nathan and Navjot continued to find the total area shaded blue using sequences of fractions. Alicia continued to use the 'ring' method, but also the summing formula to check the answers. This is Alicia's work on the other patterns:
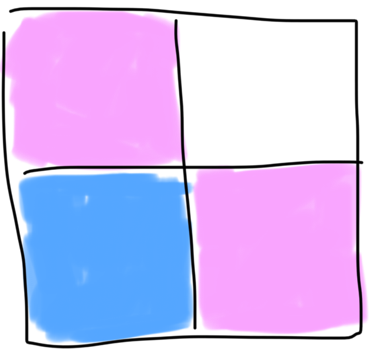
In this pattern, each smaller blue square is $\frac14$ of the area of the larger square before it. Now we just need to find the area of the first blue square. Side length is $\frac12$ of the larger square so $\frac12 \times \frac12 = \frac14.$ So the sequence of fractions whose sum represents the blue area is: $\frac14+\frac1{16}+\frac1{64}+\frac1{256} + ...$
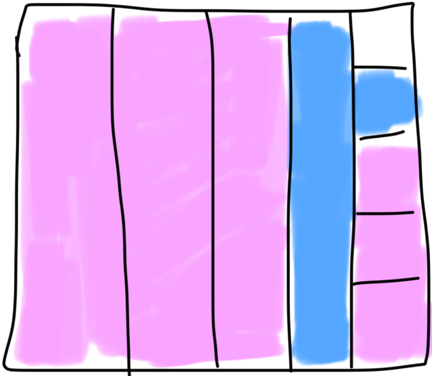
 This shows the outer ring of the pattern, in which there are two pink squares and one blue square. Since all the squares have the same area, the blue square is $\frac13$ of the total area. The same will be true for each ring added inside, therefore $\frac13$ of the overall pattern is blue.
We can check this again by summing our geometric sequence to infinity: $\dfrac{\frac14}{1-\frac14}=\frac13.$
This shows the outer ring of the pattern, in which there are two pink squares and one blue square. Since all the squares have the same area, the blue square is $\frac13$ of the total area. The same will be true for each ring added inside, therefore $\frac13$ of the overall pattern is blue.
We can check this again by summing our geometric sequence to infinity: $\dfrac{\frac14}{1-\frac14}=\frac13.$

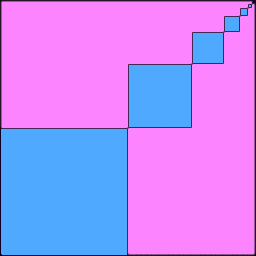
In this pattern, each T shape is $\frac6{25}$ of the area of the square around it. Each smaller ring of the pattern is $\frac1{25}$ of the area of the larger ring. So the sequence of fractions whose sum represents the blue area is: $\frac6{25} + \frac6{625} + \frac6{15625} + ...$
 This shows the outer ring of the pattern, in which the total blue area is $\frac6{24} = \frac14.$ The same will be true for each ring added, therefore a quarter of the overall pattern is blue.
This shows the outer ring of the pattern, in which the total blue area is $\frac6{24} = \frac14.$ The same will be true for each ring added, therefore a quarter of the overall pattern is blue.
The sequence of fractions whose sum represents the blue area is a geometric sequence with $a = \frac6{25}$ and $r = \frac1{25}.$ So the sum to infinity is equal to $\dfrac{\frac6{25}}{1-\frac1{25}} = \frac14.$
Alicia has used the image and the formula as two separate ways of looking at the problem. How are they linked?


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Vanishing Point
Age 14 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Navjot from Sherborne Qatar answered the questions about the first image in detail. This is Navjot's work:
Assume that its side length is $1$ unit.
Stage 1: 0, no part of the square is blue.
Stage 2: The side of the rotated blue square creates an isosceles right angled triangle with two sides being $0.5$ units (since the blue square's side touches the outer square at its side's midpoint).
So, the length of the blue square's side is: $$\sqrt{0.5^2+0.5^2}=\tfrac{\sqrt2}2$$
Blue area $=\left(\frac{\sqrt2}2\right)^2=\frac24$ of square.
Stage 3: To find the side length of the [purple] square inside the blue square, we can divide $\frac{\sqrt2}2$ by $2,$ [which gives] $\frac{\sqrt2}4$ and use this length to find the side length
by using Pythagoras' Theorem again.
Side length of innermost purple square $=\frac12,$ purple area [of the innermost purple square] $= \left(\frac12\right)^2= \frac14,$ total blue area $= \frac24 -\frac14 = \frac14$ of square.
Stage 4: Side length of innermost blue square $= \frac{\sqrt2}4,$ blue area $=\left(\frac{\sqrt2}4\right)^2=\frac2{16}$ of square.
Stage 5: Side length of innermost purple square $= \frac14,$ purple area $=
\left(\frac14\right)^2 = \frac1{16},$ total blue area $=\frac14 + \left(\frac2{16} - \frac1{16}\right) = \frac14 + \frac1{16}$
If we keep going on we will see that the area of the blue squares keep adding up in the form $\sum{\left(\frac14\right)^n}.$
Being a geometric series with a common ratio $<1,$ the summation will tend to a certain value.
Navjot then used a formula to calculate the sum of the series, and got an answer of $\frac13$. This formula was used by most people who sent in solutions to this problem and can be seen below.
For the next pattern, Alicia from Roedean School used the 'ring' method suggested in the problem. This is Alicia's work:

This shows the outer ring of the pattern. The blue rectangle is twice the area of the pink square, so there is twice as much blue as pink - $\frac13$ of the area is pink and $\frac23$ is blue. The same will be true for each ring added, therefore the overall pattern has twice as much blue as pink.
Sichao from Bangkok Patana School in Thailand found a sequence of fractions and added them up:
 As shown in the diagram the largest section shaded has area of $\frac12$ in respect to the square. The second is exactly $\frac14$ of the first; the third is also exactly $\frac14$ of the second, and so on.
As shown in the diagram the largest section shaded has area of $\frac12$ in respect to the square. The second is exactly $\frac14$ of the first; the third is also exactly $\frac14$ of the second, and so on.Therefore we know that the areas are:
$\frac 12, \frac18, \frac1{32}, \frac1{128}, ..., \frac1{2\times4^n}$
This [infinite series] we [could write as] $\sum_{n=0}^\infty{\frac1{2\times4^n}}$
To calculate the sum of terms we could rearrange the sum.
Let $S_n$ be the sum of terms.
$S_n=\tfrac12+\tfrac18+\tfrac1{32}+\tfrac1{128}+...$
$\Rightarrow 4S_n=\tfrac 42 +\tfrac48+\tfrac4{32}+\tfrac4{128}+...+\tfrac4{2\times4^n}$
$=2+S_n-\frac2{2\times4^n}$ (by substituting $S_n$)
$\Rightarrow 3S_n=2-\frac2{2\times4^n}$
As $n\rightarrow\infty,$ $\frac2{2\times4^n}\rightarrow0$ because $4^n\rightarrow\infty$
Hence $3S_n=2\Rightarrow S_n=\frac23$
Vignesh from Hymers College in the UK did this in a general case to derive a formula:
We know that the sum of an infinite geometric series is given by the equation:
$S=\frac{a}{1-r}$ (where $a$ is the first term and $r$ is the ratio)
This can be proven:
let, $$S=1+r+r^2....$$
Thus, $$ S\times r=r+r^2+r^3...\\ \Rightarrow S-S\times r=1\\
\Rightarrow S(1-r)=1\\
\Rightarrow S=\tfrac1{1-r}$$
(where $1$ is the first term and $r$ is the ratio)
This can then be applied into each of the patterns.
If the first term is $a$ instead of $1$, then the sequence is $a, ar, ar^2, ...$ and so all of the terms are multiplied by $a$. Multiplying all of the terms by $a$ has the same effect as multiplying the sum by $a$, so the formula is $S=\frac a{1-r}.$
Navjot and Nathan from Sherborne Qatar used this formula more directly. This is Nathan's work for one of the other patterns, including a description of the general strategy:


Nathan and Navjot continued to find the total area shaded blue using sequences of fractions. Alicia continued to use the 'ring' method, but also the summing formula to check the answers. This is Alicia's work on the other patterns:

In this pattern, each smaller blue square is $\frac14$ of the area of the larger square before it. Now we just need to find the area of the first blue square. Side length is $\frac12$ of the larger square so $\frac12 \times \frac12 = \frac14.$ So the sequence of fractions whose sum represents the blue area is: $\frac14+\frac1{16}+\frac1{64}+\frac1{256} + ...$
 This shows the outer ring of the pattern, in which there are two pink squares and one blue square. Since all the squares have the same area, the blue square is $\frac13$ of the total area. The same will be true for each ring added inside, therefore $\frac13$ of the overall pattern is blue.
We can check this again by summing our geometric sequence to infinity: $\dfrac{\frac14}{1-\frac14}=\frac13.$
This shows the outer ring of the pattern, in which there are two pink squares and one blue square. Since all the squares have the same area, the blue square is $\frac13$ of the total area. The same will be true for each ring added inside, therefore $\frac13$ of the overall pattern is blue.
We can check this again by summing our geometric sequence to infinity: $\dfrac{\frac14}{1-\frac14}=\frac13.$
In this pattern, each T shape is $\frac6{25}$ of the area of the square around it. Each smaller ring of the pattern is $\frac1{25}$ of the area of the larger ring. So the sequence of fractions whose sum represents the blue area is: $\frac6{25} + \frac6{625} + \frac6{15625} + ...$
 This shows the outer ring of the pattern, in which the total blue area is $\frac6{24} = \frac14.$ The same will be true for each ring added, therefore a quarter of the overall pattern is blue.
This shows the outer ring of the pattern, in which the total blue area is $\frac6{24} = \frac14.$ The same will be true for each ring added, therefore a quarter of the overall pattern is blue.The sequence of fractions whose sum represents the blue area is a geometric sequence with $a = \frac6{25}$ and $r = \frac1{25}.$ So the sum to infinity is equal to $\dfrac{\frac6{25}}{1-\frac1{25}} = \frac14.$
Alicia has used the image and the formula as two separate ways of looking at the problem. How are they linked?
- Could Alicia's work be used to derive the formula?
- Could Sichao's or Vignesh's derivation be interpreted using the 'ring' method?
You may also like
Circles Ad Infinitum
A circle is inscribed in an equilateral triangle. Smaller circles touch it and the sides of the triangle, the process continuing indefinitely. What is the sum of the areas of all the circles?
Just Rolling Round
P is a point on the circumference of a circle radius r which rolls, without slipping, inside a circle of radius 2r. What is the locus of P?
Coke Machine
The coke machine in college takes 50 pence pieces. It also takes a certain foreign coin of traditional design...

