Skip over navigation

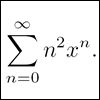

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Circles Ad Infinitum
Age 16 to 18
Challenge Level 





A circle of radius 1 cm is inscribed in an equilateral triangle. A smaller circle is inscribed at each vertex touching the first circle and tangent to the two 'containing' sides of the triangle. This process is continued ad infinitum....

What is the sum of the circumferences of all the circles?
What is the sum of their areas?
Adding all the circumferences or adding all the areas, which sum grows faster?
You may also like
Generally Geometric
Generalise the sum of a GP by using derivatives to make the coefficients into powers of the natural numbers.
Harmonically
Is it true that a large integer m can be taken such that: 1 + 1/2 + 1/3 + ... +1/m > 100 ?

