Skip over navigation
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Cubies
Age 7 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Elizabwe from Scotland sent in the following:
How many flats on each floor of the building: F 2, E 2, D 6, C 6, B 6, A2.
There are four families of 2, nine families of 3, twelve families of 4, two families of 5, one family of 6 and no families of seven.
Agatha, Charlie and Hector from Nutley CE Primary sent in the following:
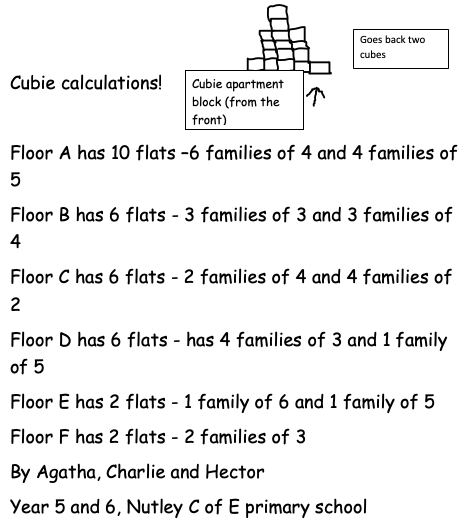
Katey Daley, a Classroom Teacher from Kelvin Grove State College in Australia send in her class' work. Below you can see two parts and the full pdf can be viewed here.


Anthony from Tirlebrook Primary School sent in his work:
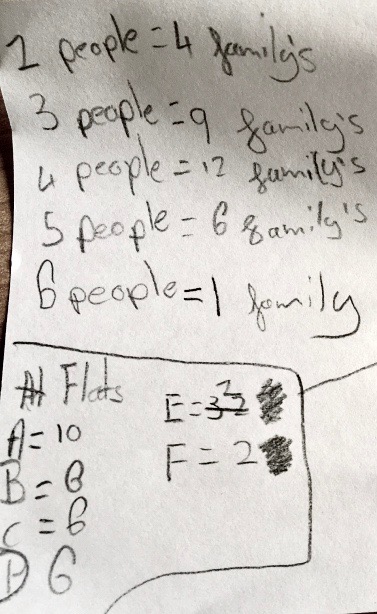
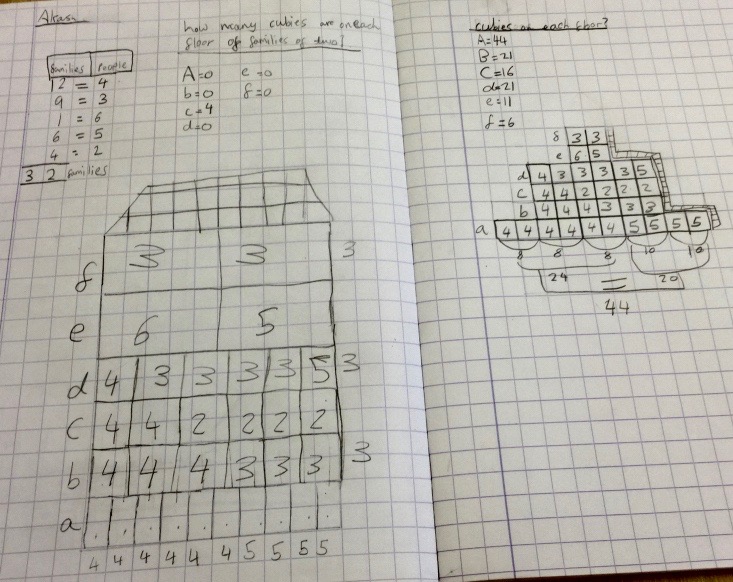
Akash from The British School of Brussels sent in an image of work done to solve this problem:
Phoebe from St Mary's Church of England Primary School Woodbridge wrote:
I found out the answers by reading the clues carefully to see which ones could be dismissed. Then I ticked the clues when I had used the information (to make it easier to see the remaining clues). I drew a picture to figure out the answers (using a pencil so I could rub out any mistakes). My proof is in the picture. This was easier than I thought when I got the hang of it.

Romilly also from St Mary's Church of England Primary School in Woodbridge wrote:
My answers are all shown in my picture. I worked out the answers by focusing on one question at a time. I read through the clues and crossed them out when I had used them. I worked out how many flats were on each floor first, then worked out how many families of each number there were. Then I could work out what the building looked like, it had to be symmetrical and the flats had to all be the same size (I used a ruler to make sure they were exactly the same size, and cubes!). Finally, I had to work out which family was where (I had to work out which floor they were on).

Frank and James Captain Elementary School in USA said:
First, we made a list of clues in a shorter format (eg. E = F # of flats). As we read the clues, we figured out that some of them were not connected to the problem we needed to solve. For example, “The bins are emptied on a Wednesday,” was not a clue that helped us figure out the number of flats, the shape of the building, the number of families or the number of cubies. This helped us eliminate clues that we didn't put in our list. After the first nine clues, we figured out how many flats were on each floor and we used wooden cubes to build a model of the block. We then drew a picture of it in our notebooks.
Once we got through 11 clues, we realized that a chart would help us keep track of the size and number of Cubie families better. Down the side, we had the names of each of the floors. Across the top, we had the possible number of cubies per family. We made a second part of the chart below the first that tracked the number of families in the block that have each different number of cubies. On the chart, we started with checks and xs to represent whether there were families of that size on that floor. As we got new clues, we replaced the checks with the number of families that size on that floor.
Finally, once we had gathered all the clues and put them in our chart, then we multiplied the number of cubies per family by the number of families that size on that floor (eg. 6 families of 4 (24) AND 4 families of 5 (20) live on Floor A, so there are 44 cubies on floor A ). After multiplying we added all the cubies on each floor to find a total population. We found that 119 cubies live in the block.
Thank you for these solutions, particularly those that have given detail about how you went about the task.
How many flats on each floor of the building: F 2, E 2, D 6, C 6, B 6, A2.
There are four families of 2, nine families of 3, twelve families of 4, two families of 5, one family of 6 and no families of seven.
Agatha, Charlie and Hector from Nutley CE Primary sent in the following:

Katey Daley, a Classroom Teacher from Kelvin Grove State College in Australia send in her class' work. Below you can see two parts and the full pdf can be viewed here.


Anthony from Tirlebrook Primary School sent in his work:
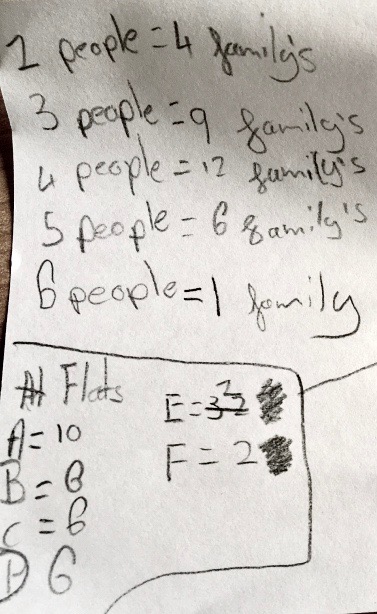
Akash from The British School of Brussels sent in an image of work done to solve this problem:

Phoebe from St Mary's Church of England Primary School Woodbridge wrote:
I found out the answers by reading the clues carefully to see which ones could be dismissed. Then I ticked the clues when I had used the information (to make it easier to see the remaining clues). I drew a picture to figure out the answers (using a pencil so I could rub out any mistakes). My proof is in the picture. This was easier than I thought when I got the hang of it.

Romilly also from St Mary's Church of England Primary School in Woodbridge wrote:
My answers are all shown in my picture. I worked out the answers by focusing on one question at a time. I read through the clues and crossed them out when I had used them. I worked out how many flats were on each floor first, then worked out how many families of each number there were. Then I could work out what the building looked like, it had to be symmetrical and the flats had to all be the same size (I used a ruler to make sure they were exactly the same size, and cubes!). Finally, I had to work out which family was where (I had to work out which floor they were on).

Frank and James Captain Elementary School in USA said:
First, we made a list of clues in a shorter format (eg. E = F # of flats). As we read the clues, we figured out that some of them were not connected to the problem we needed to solve. For example, “The bins are emptied on a Wednesday,” was not a clue that helped us figure out the number of flats, the shape of the building, the number of families or the number of cubies. This helped us eliminate clues that we didn't put in our list. After the first nine clues, we figured out how many flats were on each floor and we used wooden cubes to build a model of the block. We then drew a picture of it in our notebooks.
Once we got through 11 clues, we realized that a chart would help us keep track of the size and number of Cubie families better. Down the side, we had the names of each of the floors. Across the top, we had the possible number of cubies per family. We made a second part of the chart below the first that tracked the number of families in the block that have each different number of cubies. On the chart, we started with checks and xs to represent whether there were families of that size on that floor. As we got new clues, we replaced the checks with the number of families that size on that floor.
Finally, once we had gathered all the clues and put them in our chart, then we multiplied the number of cubies per family by the number of families that size on that floor (eg. 6 families of 4 (24) AND 4 families of 5 (20) live on Floor A, so there are 44 cubies on floor A ). After multiplying we added all the cubies on each floor to find a total population. We found that 119 cubies live in the block.
Thank you for these solutions, particularly those that have given detail about how you went about the task.

