Triangle in a Square

Thank you to everybody who sent in their ideas about this activity. Lots of children gave examples of triangles and squares which disprove Badger's last statement, and some children found ways of explaining why Badger is wrong.

Anna and Taylor from Westridge School in the USA sent us these pictures of triangles and squares:

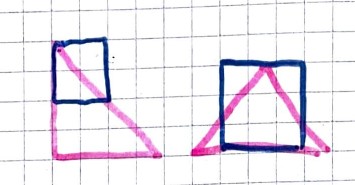
They said:

The step is wrong because a square can be smaller than a triangle but the triangle can't fit in the square.

These pictures clearly disprove Badger's fourth statement - well done. 

Safina from Halstead Preparatory School in England used a real-life analogy to explain why Badger's reasoning is wrong:

It all depends on the size of both the square and triangle.

In 3 dimensions I cannot fit the Pyramids of Giza into my dice.

That's a good point! Even though a pyramid has fewer faces than a cube, I agree that the Pyramids of Giza are definitely bigger than your dice (unless you have a very big dice).

Lots of children agreed that the sizes of the triangle and the square matter. Some children thought that the type of triangle would make a difference as well. Charlotte, Sophie and Al from Westridge School said:

Not all triangles can fit in a square because size matters. Just because the amount of sides on a triangle are smaller then a square does not mean it always fits. There are different types of triangles, such as equilateral, isosceles, and scalene, which don't all fit in squares because of the length of the sides.

Have a look at Charlotte, Sophie and Al's full solution to see if you agree.

Haleema from Pierrepont Gamston Primary School in England also thought the type of triangle would matter. She said:

Badger's statements were all true until he got to the fourth one. This is because not all triangles are equilateral (meaning equal sides and angles when it comes to geometry). For example, a scalene triangle, in which no sides or angles are the same as another, wouldn't fit because in a square, all sides and angles are the same. For the scalene triangle to fit in any shape, that shape can not be a square.

Well done to all of you for using your knowledge of triangles to come up with hypotheses about whether or not they will fit inside squares. I agree that some triangles are awkward shapes and they seem like they would stick out of the sides of a square. This would make an interesting investigation - if you draw a triangle of each different type, can you also draw a big square around it? Or are there some triangles that will never fit inside any square?

We had lots of solutions which pointed out that a very big triangle could not fit inside a very small square. Where the sizes of the triangle and square are more similar, I wonder what it is that tells us that the triangle won't fit inside the square? 

Ci Hui Minh Ngoc from Kong Hwa School in Singapore thought that it would be the area of the triangle and the square that made a difference. They said:

I can put some triangles in some squares but this is not because a triangle has fewer sides than a square. It is because of area!

This is a really good idea, Ci Hui Minh Ngoc. Is there any way of drawing a triangle inside a square where the area of the triangle is bigger? And is it possible to draw a triangle that doesn't fit inside a square even though the triangle has a smaller area than the square?

Amelie from Halstead Preparatory School thought that it would be the side length of the shapes that made a difference:

It doesn't matter about the amount of sides, only the side length of a shape. If a square has a smaller side length than a triangle, the triangle will not fit inside.

When I first read your solution I agreed with you, Amelie, but I've actually just managed to draw a triangle inside a square where one side of the triangle is longer than each side of the square. I wonder if anybody can find an example of this? Is it possible to draw a triangle inside a square where two sides of the triangle are longer than each side of the square? What about all three sides?

We also received excellent solutions from: Prayaan from King's College Junior School in the UK; Charlotte, Alyse, Charley, Kaitlyn, Xann and Stella from Westridge School; Dhruv from St. Anne's RC Primary School in the UK; Arya from Cubberley; Sion from Twyford School in the UK; Ryan from Kong Hwa School; and Teija and Fern from Pierrepont Gamston Primary School. Well done to all of you for investigating Badger's statements.