Skip over navigation
Here is a shape:
What do you know about it?
Once you've had a think, click on the buttons below to find out what some other children have said.
Cora said:
"This shape has four sides. All the sides are black."
Omar said:
"There are four corners, and the sides that connect them are all straight."
Farrah said:
"The sides of the shape are all the same length."
Dan said:
"If you drew this shape on a piece of paper, the bottom of the shape would line up with the bottom of the piece of paper."
Which of those properties tell us that this is a square?
Choose one of the facts. If we changed it, would the new shape still be a square?
Which facts are not important?
Now we're going to think about some other shape properties. Here is a new shape:
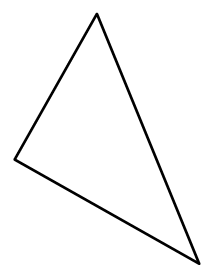
What do you know about this shape?
How would you convince someone else that what you are thinking is true?
There are more shapes in this table:
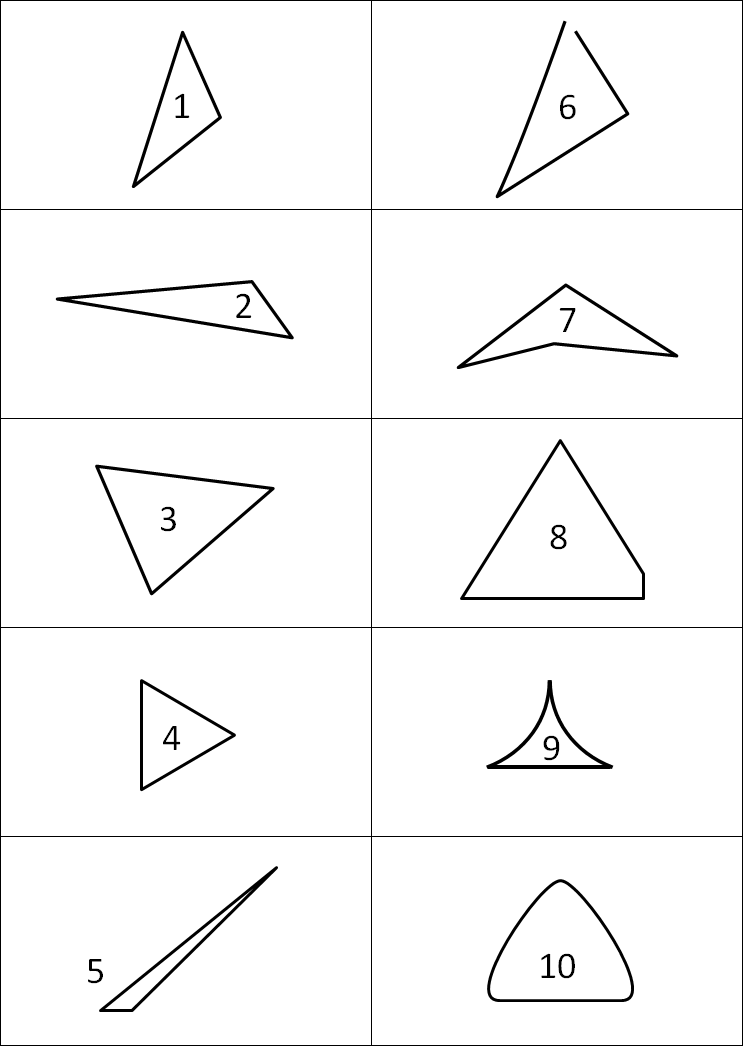
Which of these shapes are triangles?
Which aren't triangles?
How do you know?
This problem is inspired by Clements and Sarama's article 'Young Children's Ideas about Geometric Shapes', which was first published in 2000 within an NCTM journal 'Teaching Children Mathematics'. You can read the full article here.
Often, children associate the word 'triangle' with a few particular mental images, for example of a three-sided shape in a particular orientation, or of a three-sided shape with all sides of similar lengths. We should be aiming for learners to be comfortable with a definition of a triangle and refining their definition based on their mathematical experiences. The images in this task will capture children's natural curiosity and provide lots of opportunities for challenging assumptions. Discussing the characteristics of the shapes with others will improve pupils' shape vocabulary as there becomes a need to communicate efficiently.
When the children are comfortable with the idea of discussing the properties of a shape and with using a name to classify a shape, introduce a triangle picture. Ask pupils how they know it is a triangle. What properties can they see? Put the table of shapes on the board and discuss the features of some of these shapes, writing key vocabulary on the board based on the words pupils use to describe the shapes (e.g. sides, corners, straight, curved, rounded, pointy).
Once the features of some of these shapes have been discussed, give pupils the table of shapes (word, pdf) and ask them to work in pairs to make a list of the shapes which are triangles and the shapes which aren't triangles.
Bring the class back together when all pairs have finished, and discuss different answers that children have come up with. Encourage pupils to either support or challenge the ideas of others, giving reasons for their ideas. Agree as a class on which are triangles and which aren't and address any misconceptions that have arisen during the lesson.
What can you tell me about those sides?
What can you tell me about those corners?
How do you know that shape is a triangle?
How do you know that shape isn't a triangle?
For some of the shapes that aren't triangles, pupils might be able to work out what the real name would be.
Children could make a poster about triangles, drawing their own examples of triangles and shapes that aren't triangles.
The task Name That Triangle! could follow on from this one. It involves classifying triangles according to side length and angles.
Pupils might want to cut out the shapes in order to see them in different orientations.
Some children might benefit from having a selection of plastic triangle shapes to compare with the pictures.
Triangle or No Triangle?
Age 5 to 7
Challenge Level 
Triangle or No Triangle?
Here is a shape:
What do you know about it?
Once you've had a think, click on the buttons below to find out what some other children have said.
Cora said:
"This shape has four sides. All the sides are black."
Omar said:
"There are four corners, and the sides that connect them are all straight."
Farrah said:
"The sides of the shape are all the same length."
Dan said:
"If you drew this shape on a piece of paper, the bottom of the shape would line up with the bottom of the piece of paper."
Which of those properties tell us that this is a square?
Choose one of the facts. If we changed it, would the new shape still be a square?
Which facts are not important?
Now we're going to think about some other shape properties. Here is a new shape:
What do you know about this shape?
How would you convince someone else that what you are thinking is true?
There are more shapes in this table:
Which of these shapes are triangles?
Which aren't triangles?
How do you know?
This problem is inspired by Clements and Sarama's article 'Young Children's Ideas about Geometric Shapes', which was first published in 2000 within an NCTM journal 'Teaching Children Mathematics'. You can read the full article here.
Why do this problem?
This activity provides an engaging context for younger children to deepen their understanding of properties of shapes and, in particular, what makes a triangle a triangle. Discussing the introductory task, which focuses on properties of squares, may uncover misconceptions about the relationship between rectangles and squares. (All squares are rectangles.)Often, children associate the word 'triangle' with a few particular mental images, for example of a three-sided shape in a particular orientation, or of a three-sided shape with all sides of similar lengths. We should be aiming for learners to be comfortable with a definition of a triangle and refining their definition based on their mathematical experiences. The images in this task will capture children's natural curiosity and provide lots of opportunities for challenging assumptions. Discussing the characteristics of the shapes with others will improve pupils' shape vocabulary as there becomes a need to communicate efficiently.
Possible approach
Begin with some large 2D shapes on the board. Pick one of the shapes (e.g. a square) and ask children to discuss what properties they can see. What properties are needed for us to call that shape a square? If we tilted it, would it still be a square? Why/why not?When the children are comfortable with the idea of discussing the properties of a shape and with using a name to classify a shape, introduce a triangle picture. Ask pupils how they know it is a triangle. What properties can they see? Put the table of shapes on the board and discuss the features of some of these shapes, writing key vocabulary on the board based on the words pupils use to describe the shapes (e.g. sides, corners, straight, curved, rounded, pointy).
Once the features of some of these shapes have been discussed, give pupils the table of shapes (word, pdf) and ask them to work in pairs to make a list of the shapes which are triangles and the shapes which aren't triangles.
Bring the class back together when all pairs have finished, and discuss different answers that children have come up with. Encourage pupils to either support or challenge the ideas of others, giving reasons for their ideas. Agree as a class on which are triangles and which aren't and address any misconceptions that have arisen during the lesson.
Key questions
How many sides does that shape have?What can you tell me about those sides?
What can you tell me about those corners?
How do you know that shape is a triangle?
How do you know that shape isn't a triangle?
Possible extension
For some of the shapes that aren't triangles, pupils might be able to work out what the real name would be.Children could make a poster about triangles, drawing their own examples of triangles and shapes that aren't triangles.
The task Name That Triangle! could follow on from this one. It involves classifying triangles according to side length and angles.
Possible support
Pupils might want to cut out the shapes in order to see them in different orientations.Some children might benefit from having a selection of plastic triangle shapes to compare with the pictures.
You may also like
Let's Investigate Triangles
Vincent and Tara are making triangles with the class construction set. They have a pile of strips of different lengths. How many different triangles can they make?
Three Fingers and a Loop of String
Using a loop of string stretched around three of your fingers, what different triangles can you make? Draw them and sort them into groups.