Guess What?
Guess What?
This game, for two players, is based on the popular game 'Guess Who?'.
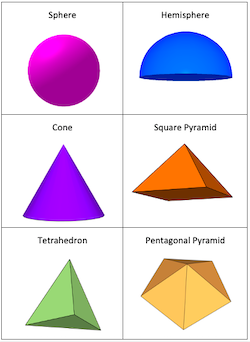
Each player needs:
- a printed copy of these sheets, cut up into individual cards, each one picturing a 3D shape
- a printed copy of this single sheet, showing all the 3D shapes
- a pencil.
The aim of the game is to guess which shape your partner has chosen before they guess the shape you have chosen.
How to play:
- Each player chooses one of the shapes on the single sheet and marks it somehow, for example using a pencil tick. (If the sheet is laminated, you could use a whiteboard pen.) This is the shape that your opponent is trying to guess.
- Each player lays out all their cards face-up in front of them.
- Player 1 asks player 2 a question to try to find out information about the shape player 2 has chosen. Player 2 can only answer yes or no in response.
- Based on player 2's answer, player 1 turns face-down any shape cards that they now know can't have been chosen by player 2.
- Player 2 now asks player 1 a question in a simillar way.
- The winner is whichever player finds out their opponent's shape first.
Try playing the game lots of times.
What questions are the 'best' to ask in order to find out your opponent's shape before they guess yours? Why are they good questions?
We would love to hear about the questions that work well for you!
Why play this game?
Not only will this game give learners meaningful practice in using geometrical vocabulary and help familiarise them with characteristics of 3D shapes, but it will also encourage them to think flexibly and adapt their approach when they get stuck.
You can read more about developing mathematical flexibility through geometry in this article.
Possible approach
You could introduce the class to the main idea of this game by playing an adapted version against them. Display this sheet on the board so that all the shapes are visible without the need to scroll. Explain to the group that you are choosing one of these shapes, and mark it on a printed copy of the sheet. Turn over the sheet so that it is not visible. Explain that the group must find out which shape you have chosen by asking questions which you can only answer with yes or no. You could invite learners to talk in pairs about what they would ask first, and then ask one pair to pose their question. When you have answered it, suggest the pair come up to the board and cross out all the shapes that cannot be yours. Continue in this way until the class has identified your shape.
You can now set them off in pairs playing the game using a set of the cards and a opy of the printable sheet each. (If both the cards and the sheets are laminated they could be reused.) Allow time for them to get a good feel for the game before drawing the whole group together again and suggesting that now they play in fours - one pair against another. Ask them to be thinking about 'good' questions to ask which help them narrow down the possibilities quickly. Playing in pairs offers the opportunity to discuss this strategic element with someone else before having to commit to asking a particular question.
The final plenary can focus on sharing some of the 'best' questions and, in particular, helping learners articulate their reasoning for choosing each question. It can be useful to share instances when learners identified pointless questions too and the reasons why those question did not reveal extra information.
Key questions
What is the same about some of these shapes?
What is different about them?
How could these similiarities and differences help us come up with a question?
Possible extension
You could challenge children to find out the smallest number of questions that will identify a single shape. The number of questions may well depend on the shape that is chosen...
Possible support
These cards depict fewer shapes and might be useful for some children. Here is the associated single sheet to print. All learners will benefit from real examples of these solid shapes to handle at various points throughout the lesson, should they wish.
You may also like
Add 3 Dice
Three dice are placed in a row. Find a way to turn each one so that the three numbers on top of the dice total the same as the three numbers on the front of the dice. Can you find all the ways to do this?
Online
A game for 2 players that can be played online. Players take it in turns to select a word from the 9 words given. The aim is to select all the occurrences of the same letter.