Let's Get Flexible with Geometry

If learning mathematics is going to be an exciting adventure for our young learners, then we need to ensure that they experience sufficient opportunities to enjoy working flexibly across the mathematics curriculum. Being flexible enables them to appreciate that problems may have more than one possible answer, become more willing to consider alternative strategies when they get stuck (rather than simply giving up!) and begin posing their own problems for others to enjoy. In this article, we'll explore a selection of engaging activities for developing mathematical flexibility through geometry.

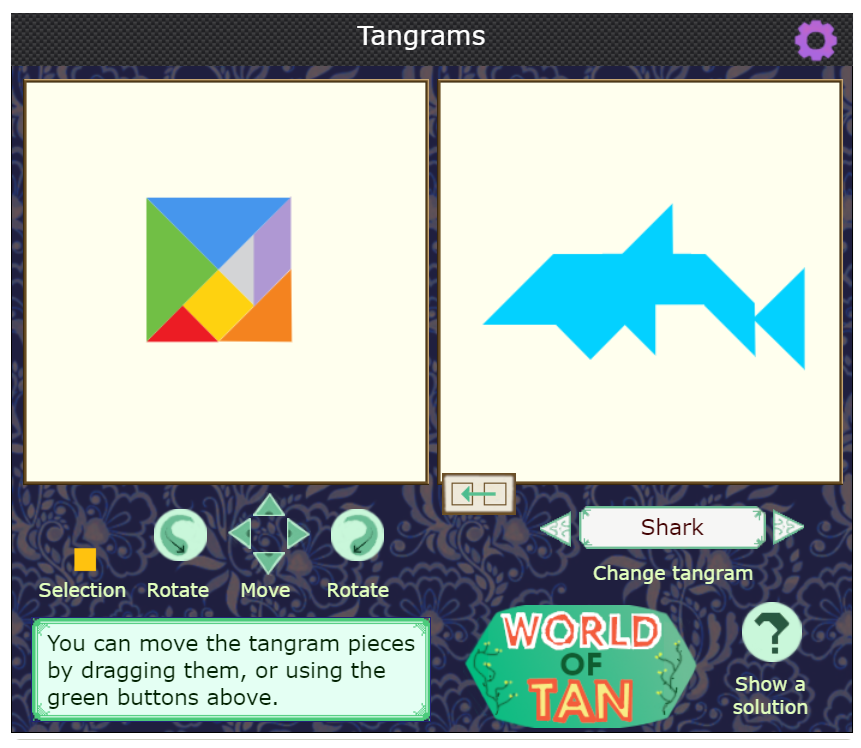
Tangrams offer a fantastic starting point for nurturing flexibility in our primary classrooms. Many young learners relish recreating tangram designs, but they also derive great pleasure from setting their own challenges for others to solve. This enables them to develop their strategic competence as they begin to move from being problem-solvers to becoming problem-posers too. In our Tangram Browser, they can explore tangrams with a very engaging interactivity whilst consolidating their knowledge about triangles, squares and parallelograms.

The Tangram Browser enables young learners to put into practise their visualising skills and develop their willingness to work flexibly to consider where the different shapes might go before trying out their ideas. When combining shapes to complete the picture, they will use their emerging understanding of translations, reflections and rotations to decide how to transform them. There are also links between tangrams and fractions, and they can be encouraged to work out what fraction of the whole square is represented by each smaller shape. Story-telling is a lovely way to introduce young learners to Tangrams, and you'll find a host of story-linked tangram activities in our World of Tan series of activities. 

As well as maximising the potential of tangrams, exploring patterns is another useful approach for supporting flexibility among young learners. For example, Repeating Patterns offers the opportunity to recognise, make and describe repeating patterns of triangles, and then challenges young learners to create repeating patterns of their own.

Another useful approach for encouraging flexibility in the mathematics classroom is limiting the initial amount of information given to the learners. For example, initially asking them to draw a quadrilateral can result in a huge variety of four-sided shapes before we provide them with further clues, enabling them to narrow their answer to a single shape, such as a rhombus. This is the approach taken in our Shape Draw activity; working in small groups, each learner has one or more clue cards and they need to work together to identify which shape satisfies all of the clues on their cards. Hannah, from St Peter's Catholic School, shared her flexible approach towards finding the answer for Shape Draw, "I tried a kite shape at first, but it didn't work. Then, I thought a rectangle... " Hannah's wilingness to adapt her approach based on the information given on the cards enabled her to successfully identify the correct shape. Using clue cards is a lovely way to encourage flexible thinking, and the activity can be extended by encouraging young learners to write their own set of similar cards for others to enjoy.                                    

Some of the most engaging geometry problems for primary learners have more than one possible answer. Imagine, using the light from a visualiser, they could see only see the shadow of circle. Which 3D shapes do they think might have created that circle, and why? 

William from Swanbourne House school suggested several possible 3D shapes with at least one circular face: "The black circle could be a sphere, hemisphere, cylinder or cone." This type of activity, which encourages young learners to consider more than one solution to a problem and to justify their reasoning, inspired our Shadow Play activity. As well as encouraging them to consider more than one possible answer to a problem, Shadow Play is also a very useful activity for reinforcing the names and characteristics of both 2D and 3D shapes.

Although we can encourage our classes to actively engage with exciting problems, sometimes their initial choice of approach does not work. We need to support young learners to develop a willingness to embrace different ways of working when they get stuck, rather than simply giving up. Having alternative strategies enables them to develop their resilience and perseverance. With young learners, geometrical activities are an ideal platform for developing these key skills. Consider the classic game 'Guess Who?' which challenges young learners to narrow down a large number of possibilities to a single answer. To be successful, they need to adapt their questioning based on the response to the previous answer. We've embraced this approach by developing our child-friendly, geometrical version of the game, Guess What?. Taking into account the different expectations of the primary geometry curriculum, we have devised two different versions of the shape cards. (You can find the more accessible set of cards linked in the Teachers' Resources section of the task.) 

In our feature Flexibility in Geometry, of which this article is a part, you willl find a range of tasks (some of which are mentioned above) to support you in encouraging learners to work flexibly across a range of geometrical activities. We hope you enjoy many geometric journeys with your learners.

Reference

Kilpatrick, J., Swafford, J., & Findell, B. (2001). Adding it up: Helping children learn mathematics (Vol. 2101). National research council (Ed.). Washington, DC: National Academy Press.