Digital Equation

Let $k$ be an integer satisfying $0\le k \le 9\,$. Show that $0\le 10k-k^2\le 25$.

Mal from Bedford School in the UK and Mahdi from Mahatma Gandhi International School in India tried all the possible values of $k.$ Here is Mal's work:

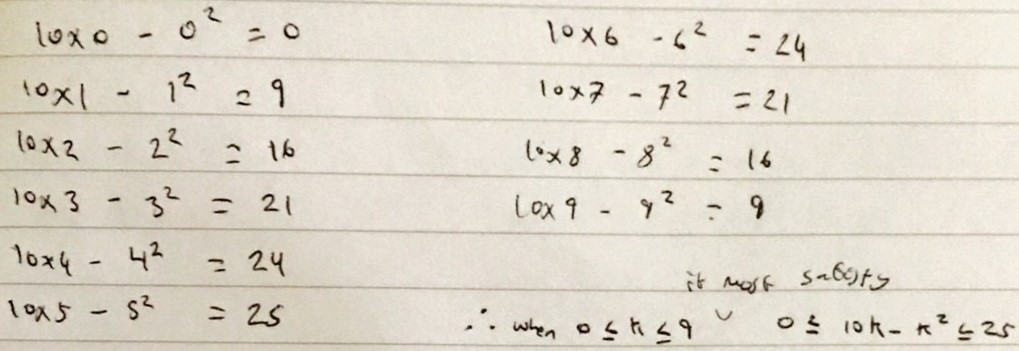
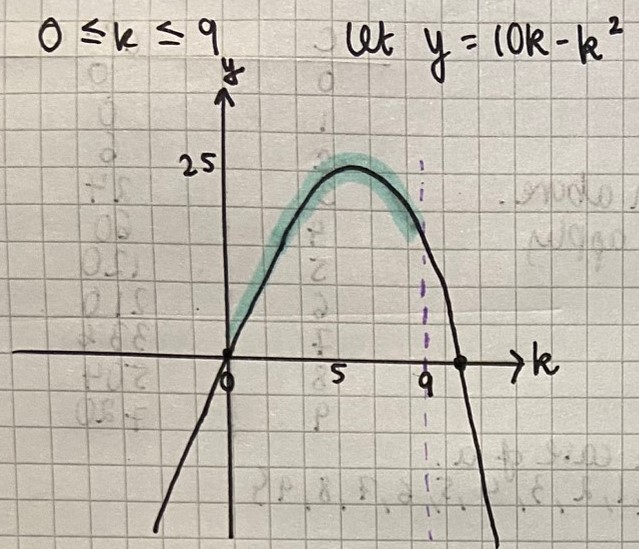
Nikita from Jersey College for Girls, Mohamed S from LAE Tottenham in the UK and Sanika from PSBBMS, OMR in India used a graph. The sketch is from Nikita's work. This is how Sanika found the roots and the maximum value:

$y=f(x)=x(10-x)$

The roots of the equation are 0 and 10.

Since the squared term has a negative coefficient the parabola will face downwards.

The highest y-coordinate will therefore be in the first quadrant with an x value right between the two x intercepts. (As quadratic equations have symmetric graphs). This implies that the x coordinate is (0+10)$\div$2 = 5. 

Substituting this value into the function $f(x)$ will give us the y coordinate; this will be the highest output of the function.

$\therefore 25\geq k(10-k)$

If the condition that $0\leq k\leq9$ is considered, then it can be concluded that the lowest y-coordinate is obtained when the x-coordinate is $0$ $\therefore 0\leq k(10-k)$

Nikita found the maximum value by completing the square: 

$y=-(k-5)^2+25$
so max point is at $(5,25)$

Mohamed S found the maximum value using differentiation:

$f'(k) = 10-2k$
To find maximum:
$10-2k=0$
$10=2k$
$k=5$
$10\times5 - 5^2 = 25$
$25$ is the maximum

Wiktor from LAE Tottenham and David from the UK proved the inequality algebraically. This is David's work:

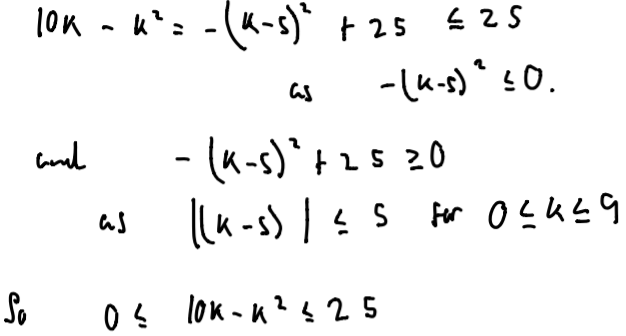
Sanika also proved the inequality using the arithmetic mean - geometric mean inequality:

AM-GM inequality: $\dfrac{a+b}2 \geq \sqrt{ab}$

Applying AM-GM to the numbers $k$ and $(10-k)$ we get the following: $$\frac{k+(10-k)}2 \geq \sqrt{k(10-k)} \Rightarrow 25\geq k(10-k)$$ The expression will always give a positive integer as output if $0\lt k \leq 9\,.$ So the lowest value can be obtained when $k=0\, .$
 

Show also that $k(k-1)(k+1)$ is divisible by $3\,$.

Mal checked this for the integers 1 to 9:

David, Wiktor, Mohamed S, Mahdi and Nikita wrote this simple proof (this is Wiktor's work):

Nikita and Sanika considered different cases. This is Nikita's work:

For each $3$-digit number $N$, where $N\ge100$, let $S$ be the sum of the hundreds digit, the square of the tens digit and the cube of the units digit. Find the numbers $N$ such that $S=N$.

Nikita, David, Mal, Wiktor, Mohamed S, Sanika and Mahdi found an equation linking $a,b$ and $c\,.$ This is Nikita's work:

Nikita then found the possible values of $c^3-c$ and went through the values of $a$ to find solutions.

Wiktor and David used part 1 to find out more about $b$. This is Wiktor's work:

Mohamed wrote:

This means that a multiple of $99$ minus a number between $0$ and $25$ must be equal to $c(c+1)(c-1).$ $99a$ must be close to $c(c+1)(c-1)$ but smaller.

Mahdi, Mohamed, Wiktor and Mal used this idea to go through the possible values of $c$. This is Mahdi's work:

Using all the information, Sanika made a table showing the possible values of $a, b$ and $c$:

After a couple of combinations, 4 numbers can be derived:
175
135
518
598