Clock Arithmetic

You may be familar with a straight number line, but what happens if we change the rules and make our number line into a circle?

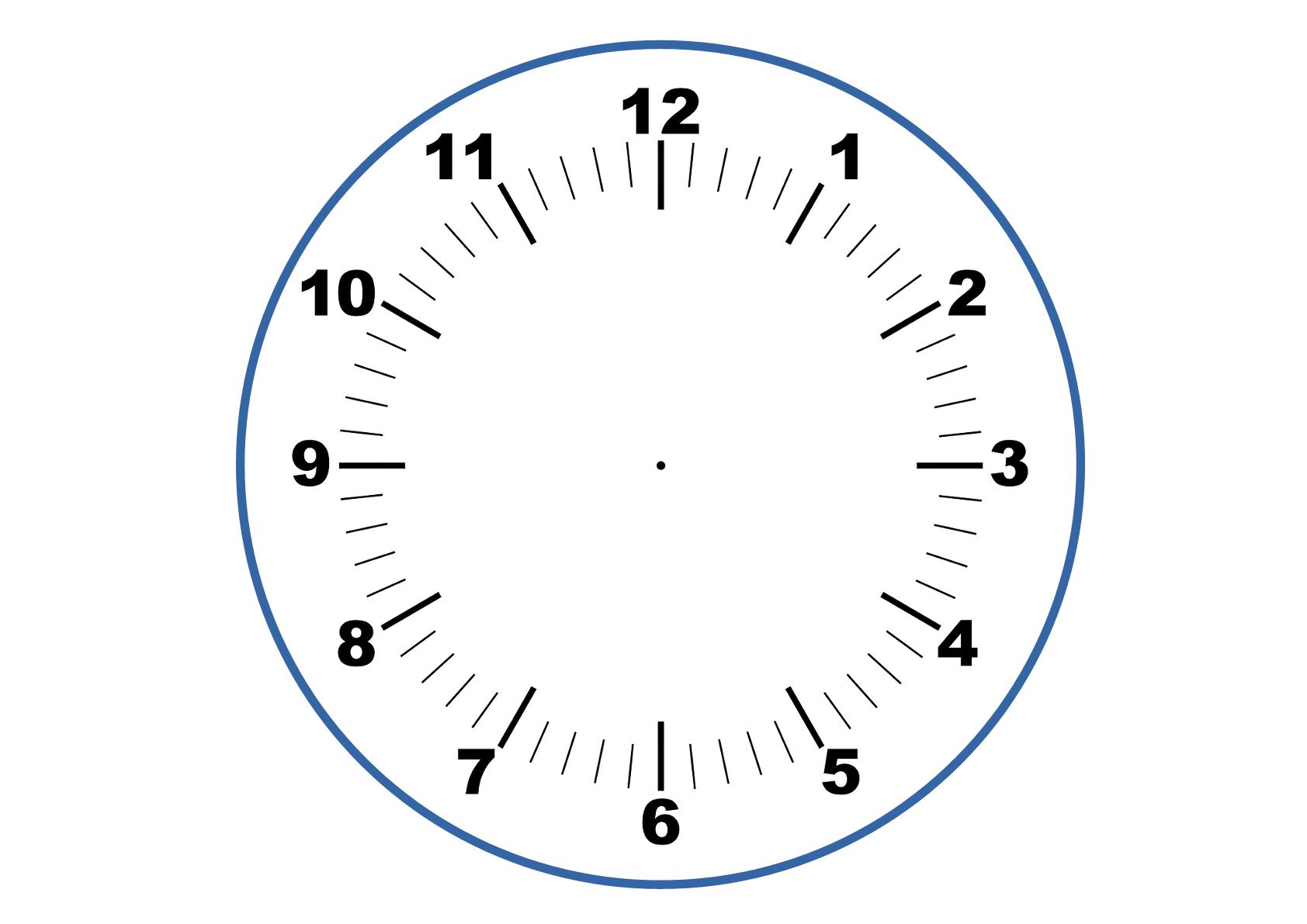
We are used to using this sort of arithmetic when we use clocks.  

The numbers go from 1 to 12, but when you get to "13 o'clock", it actually becomes 1 o'clock again (think of how the 24 hour clock numbering works). So 13 becomes 1, 14 becomes 2, and so on.

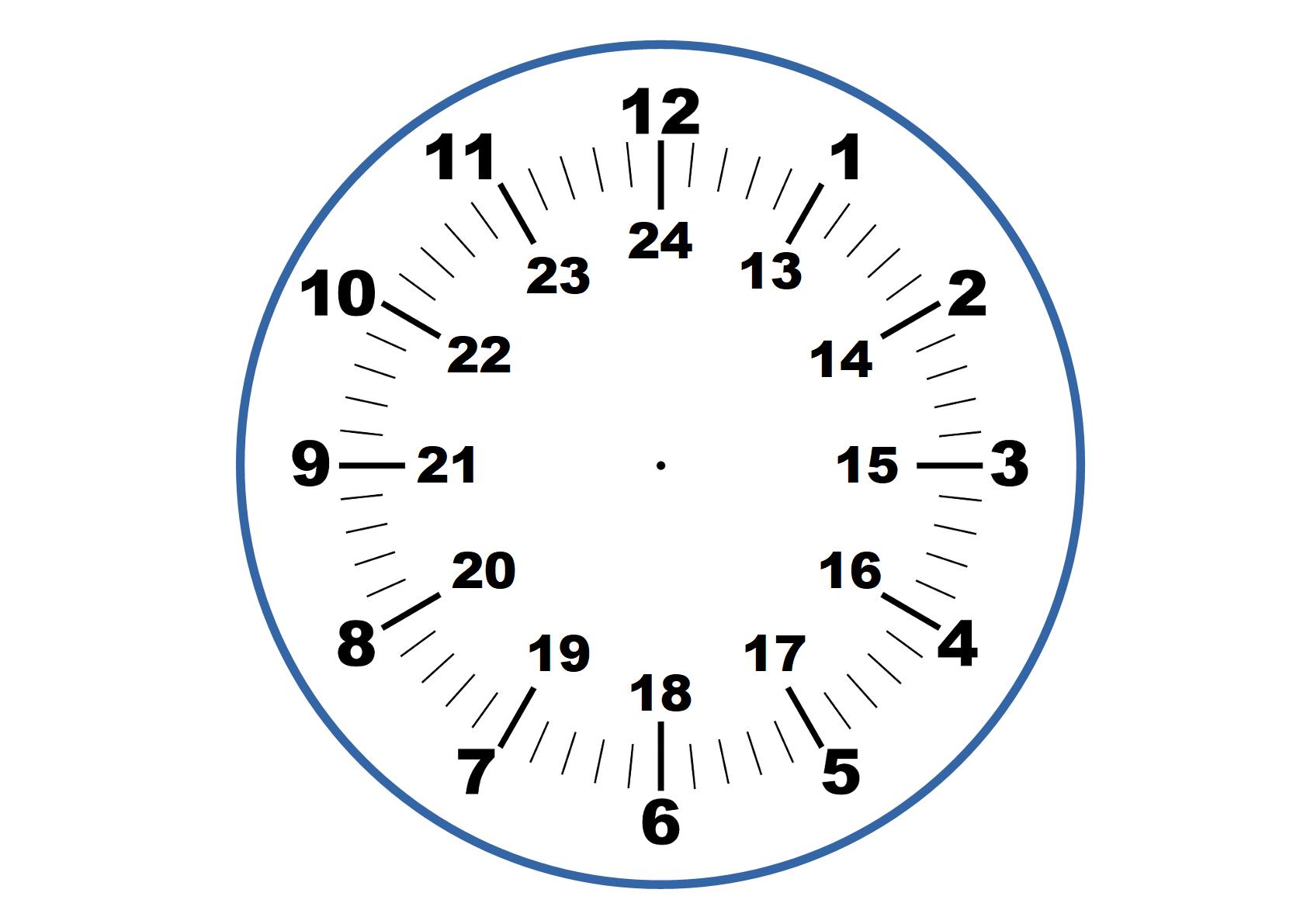
This can keep going, so when you get to "25 o'clock'', you are actually back round to where 1 o'clock is on the clock face (and also where 13 o'clock was too).

Click on "Task 1" to find the first set of questions.  Once you have tried these you can check your solutions.

You may have noticed that everytime you add $12$ hours you end back where you were, so instead of adding on 30 hours you can use the fact that $30=12+12+6$ and so just add on $6$ hours instead.

We write $30 \equiv 6 \text{ mod } 12$ which reads as "$30$ is congruent to $6$ mod (or modulo) $12$".

Instead of using the 12 numbers of a clock, we could instead take the portion of the number line between 0 and 7 inclusive and wrap this into a circle so that the 0 and 7 are in the same place (and we write 0 in this position).

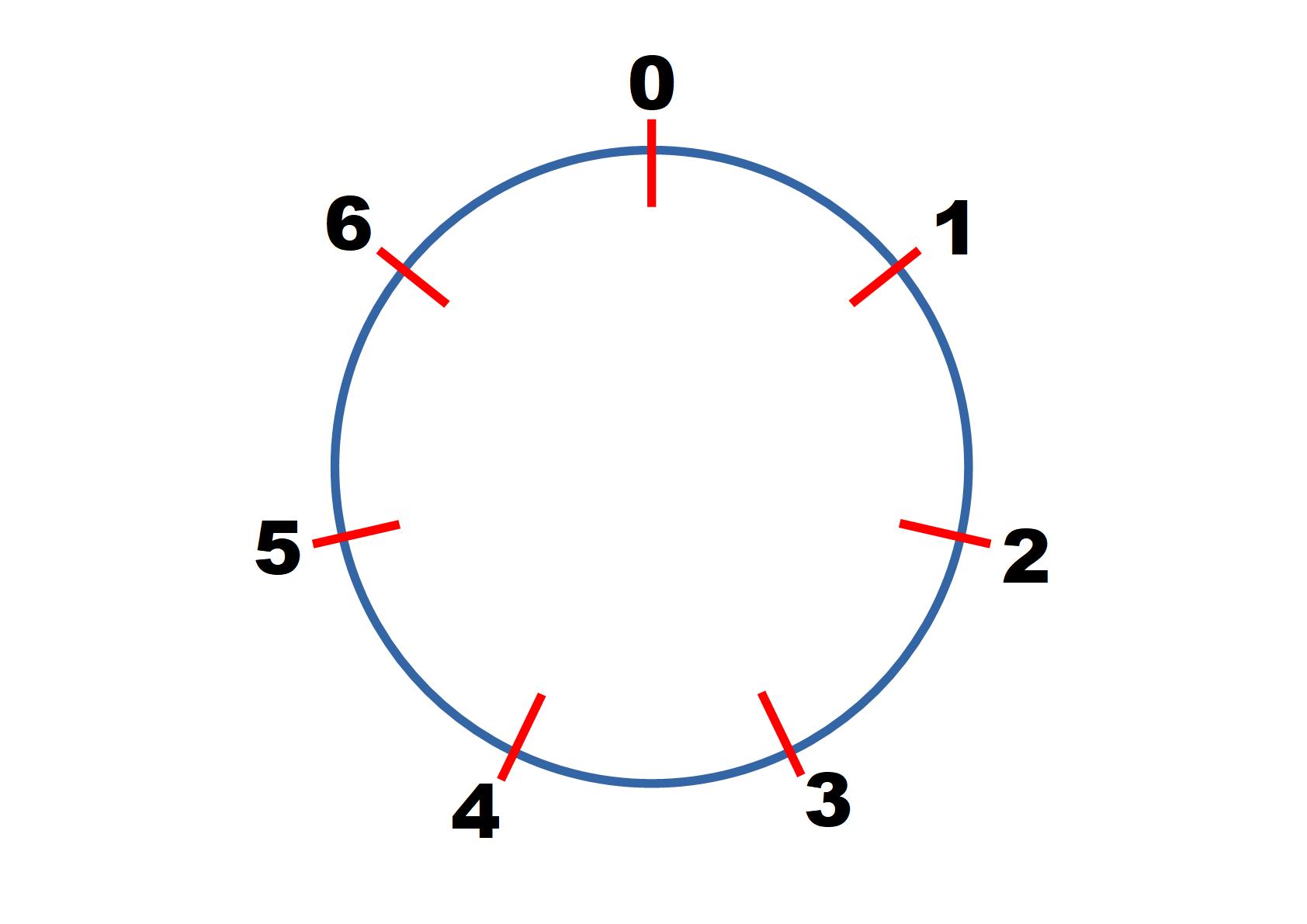
You can still use this curved number line to calculate sums like "3+2" but instead of "+2" meaning move two places to the right, it means moving 2 places "clockwise".   When working with this clock you are working in modulo 7 (there are 7 numbers, including 0, around the clock), so you would write $4+5 \equiv 2 \text{ mod } 7$.

Subtracting can be thought of as a move anticlockwise around the circle.  Can you work out the answers to these?

When using clock arithmetic, subtracting is not really necessary, as instead of moving round anticlockwise we can move clockwise and end up in the same position. We have $1 - 2 \equiv 6$ mod $7$ but we also have $1 + 5 \equiv 6$ mod $7$. This means that the operation "$-2$" is equivalent to "$+5$" when we are working modulo $7$.

We can also keep travelling round our modulo $7$ clock. If we wanted to represent $16$ we would start at $0$ and move $16$ places clockwise until we ended on $2$. We would write $16 \equiv 2 \text{ mod }7$.

You can use some of these ideas to solve problems about days of the week. 

Can you use your knowledge of arithmetic modulo 7 to solve this final set of problems?

If you have enjoyed working on this problem, then you may enjoy More Adventures with Modular Arithmetic and Clock Squares 

We are very grateful to the Heilbronn Institute for Mathematical Research for their generous support for the development of this resource.