More Adventures with Modular Arithmetic

This problem follows on from Clock Arithmetic.

Start by considering arithmetic modulo 7.

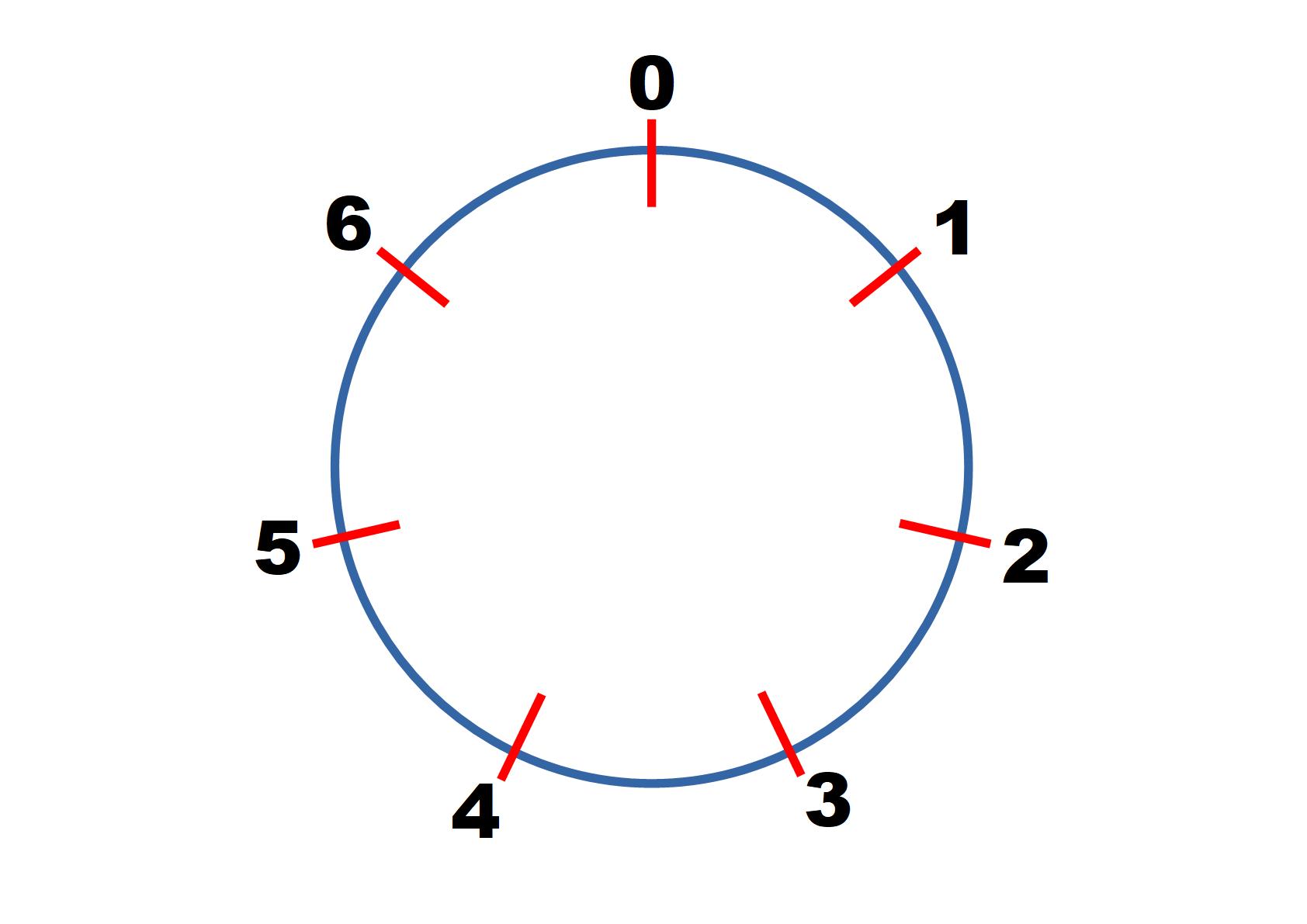
Consider $20 \text{ mod } 7$, $60 \text{ mod 7}$ and $80 \text{ mod 7}$. 
Is $80 \text{ mod } 7$ the same as $20 \text{ mod } 7 + 60 \text{ mod } 7?$

Consider other pairs of numbers $A \equiv a \text{ mod } 7$ and $B \equiv b \text{ mod }7$. 
Is it always true that $A+B \equiv (a + b) \text{ mod } 7?$

What if we have $A \equiv a \text{ mod }n$ and $B \equiv b \text{ mod }n?$

Consider $4 \text{ mod } 7$, $20 \text{ mod 7}$ and $80 \text{ mod 7}$. 
Is $80 \text{ mod } 7$ the same as $(4 \text{ mod } 7)\times (20 \text{ mod } 7)$?

If $A \equiv a \text{ mod }n$ and $B \equiv b \text{ mod }n$ is it always true that $AB \equiv ab \text{ mod }n$?  Can you use the proof sorter for $A+B$ to help you construct a similar proof for $A \times B$?  Once you have tried this, click the button below to compare your proof to ours.

Equations with modulo arithmetic

Consider the equation $3x \equiv 1 \text{ mod } 7$ where $x<7$.  By considering $x=0, 1, ... , 6$ find a possible value of $x$. 

Find numbers that solve $3x \equiv b \text{ mod } 7$ for $b=2, 3, 4, 5, 6$.

Find numbers that solve $6x \equiv b \text{ mod } 7$ for $b=1, 2, 3, 4, 5, 6$.

Find numbers that solve $4x \equiv b \text{ mod } 10$ for $b= 1, 2, ... , 9$.

Can you find a number $a$ so that $ax \equiv b \text{ mod } 10$ has a solution for every $b=1, 2, ... , 9$?

You should have discovered that sometimes it is possible to find solutions to modular arithmetic equations, and sometimes it isn't.  The interactivity below can be used to model what is happening when finding multiples of a number in different modulos.

You can change the number of dots by using the slider (which represents the modulo we are working in). Choose a starting point and drag to another point, then see what happens as the jumps are repeated.
For example, to model $4x \equiv b \text{ mod }10$, you can change the number of dots to $10$ and then drag between two dots which are 4 spaces apart.  This shows that only 5 out of the 10 dots are visited, which shows that $4x \equiv b \text{ mod }10$ only has solutions for 5 values of $b$. 

Investigate other equations of the form $ax \equiv b \text{ mod } n $, where $0 \le x \le n-1$.
Can you find a condition for solutions to exist?
Can you find a way of working out how many solutions there are?

If you have enjoyed working on this problem, then you may enjoy Euler's Totient Function.

We are very grateful to the Heilbronn Institute for Mathematical Research for their generous support for the development of this resource.