More Adventures with Modular Arithmetic

Olivia from Roedean in the UK tried different values of $x$ to solve the equations $3x \equiv 1 \text{ mod } 7$ and $3x \equiv b \text{ mod } 7$:

Mahdi from Mahatma Gandhi International School in India used the rules proved earlier in the problem:

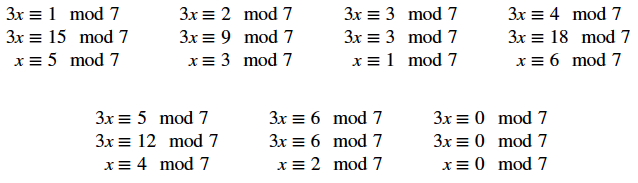
For the equation $6x \equiv b \text{ mod } 7$, Olivia wrote:

Mahdi wrote:

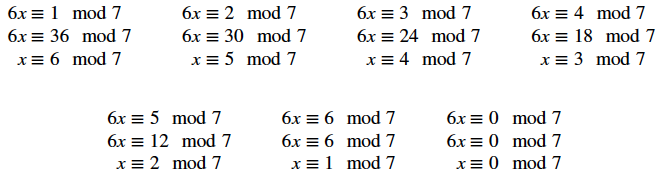
Since $7$ is prime, for every value of $a$ and $b$, there is a unique solution for $x$ in the equation $ax\equiv b \text{ mod 7}$

For the equations $4x \equiv b \text{ mod } 10$ and $ax \equiv b \text{ mod } 10$, Olivia wrote:

To find numbers that solve $4x \equiv b \text{ mod } 10$, we make a table again

Mahdi wrote:

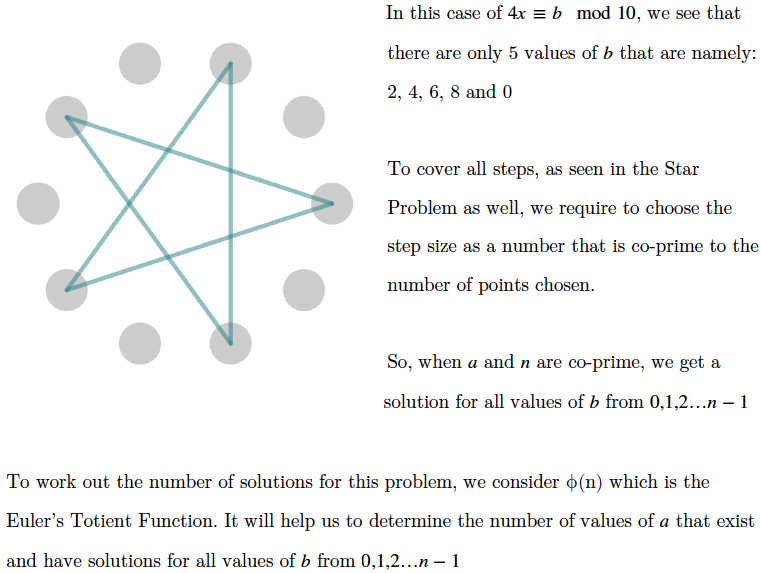
The problem that Mahdi mentions is Stars. Olivia also used the interactivity to explain how to choose possible values of $a$:

Considering the proof that, when $A \equiv a \text{ mod }n$ and $B \equiv b \text{ mod }n$ it is always true that $AB \equiv ab \text{ mod }n$, Amy asked whether this proof could be adapted to find which values of $a$ and $b$ give solutions to the equation $ax \equiv b \text{ mod }n$.

Since the proof shows that the first rule is true for all $a$ and $b$, but later we want to find the specific values of $a$ and $b$ which give solutions, one cannot be adapted easily to give the other. However, a similar argument can be used to demonstrate which values of $a$ and $b$ will work for each $n$.

This is linked to Mahdi's first method. Consider applying Mahdi's first method to $4x\equiv b \text{ mod 10}$:

$4x \equiv 2\text{ mod 10}$
$\Rightarrow 4x \equiv 12\text{ mod 10}$
$\Rightarrow x  \equiv 3\text{ mod 10}$

However
$4x \equiv 1\text{ mod 10}$
$\Rightarrow 4x \equiv 11\text{ mod 10}\equiv 21,31, 41, 51, ...\text{ mod 10}$
And none of those numbers are divisible by $4$.

Can you generalise this?