Euler Meets Schlegel

You might like to work on the problem Network Trees first.

A network consists of points (vertices) and lines between them (edges).  A planar network is one where the edges do not cross each other, or which can be redrawn so that the edges do not cross. A connected network is one where you can travel to any vertex to any other vertex along the edges of the network.

A connected planar network (which has been redrawn if necessary so that edges do not cross) splits up the plane in which it lies into regions.  The picture below shows a network which is dividing the plane into 6 regions (the space "outside" or "around" the network is counted as a region).

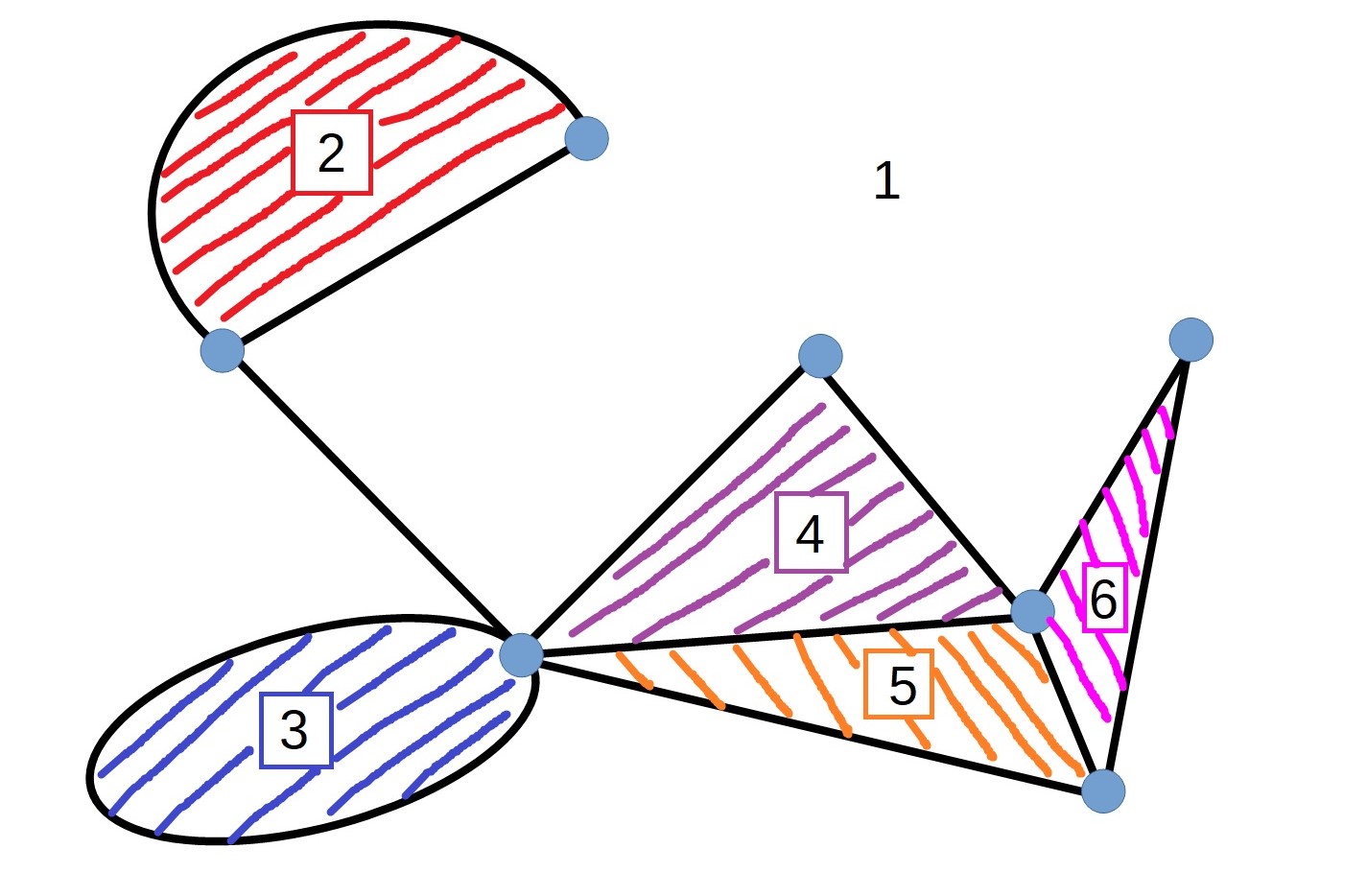
How many vertices, regions, and edges are there for this network?

Draw some different connected planar networks and count the number of 
vertices (V), edges (E) and regions (R).
Can you find a rule connecting V, R and E ? (known as Euler's formula)
Can you explain why the rule works?

Schlegel Diagrams

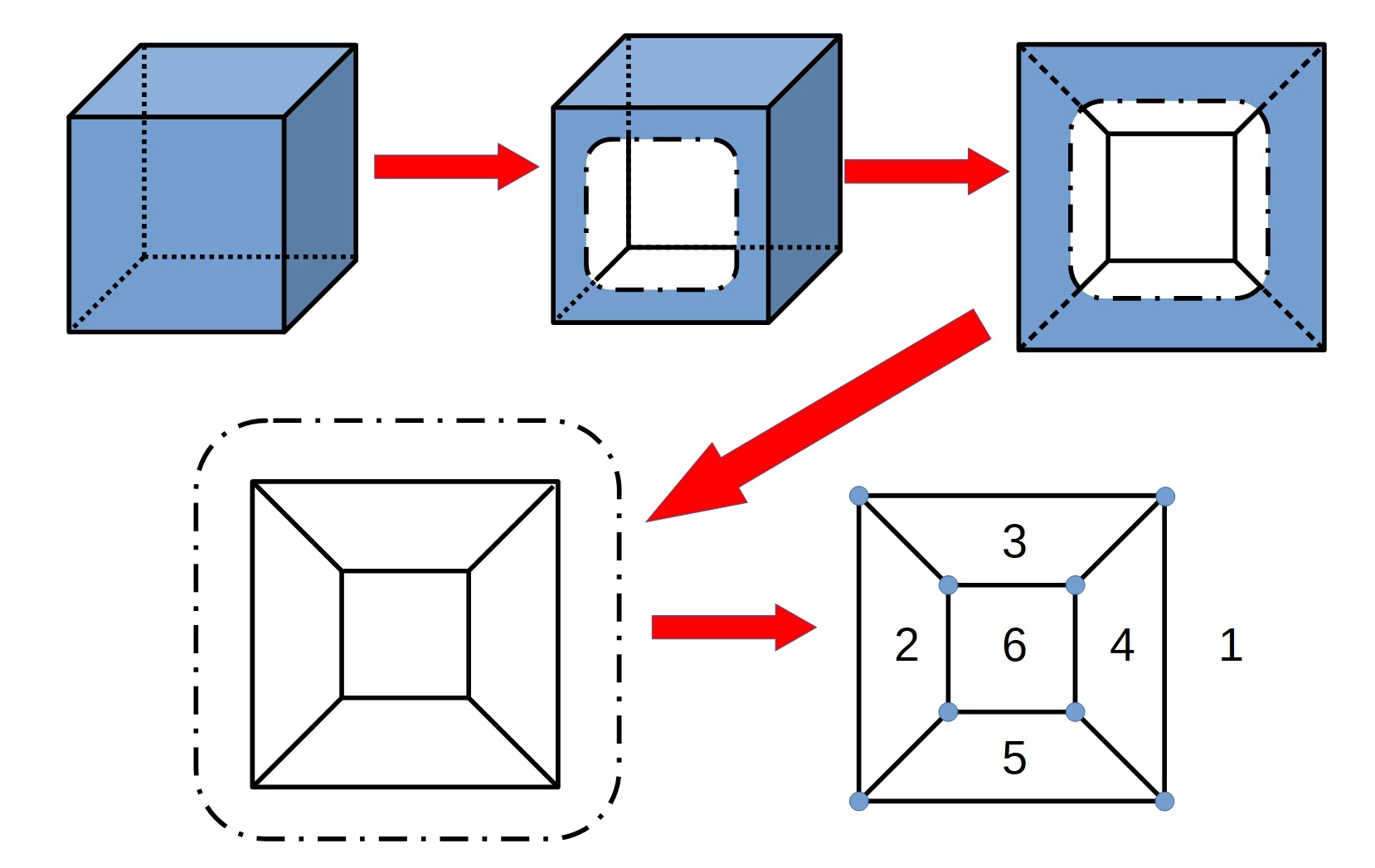
This result for networks can also be applied to polyhedra.  We can represent every polyhedron as a network using something called a Schlegel diagram.  Consider a cube - we can imagine cutting a hole in a face, and then opening out this cut face and flattening the cube out (imagine the cube is made out of a flexible material so that we can stretch and manipulate it). 

The resulting network has the same number of vertices and edges as the cube, and the number of regions in the network is the same as the number of faces of the cube.

For a triangular prism, we can consider cutting into a triangular face or into one of the rectangular faces, as shown below:

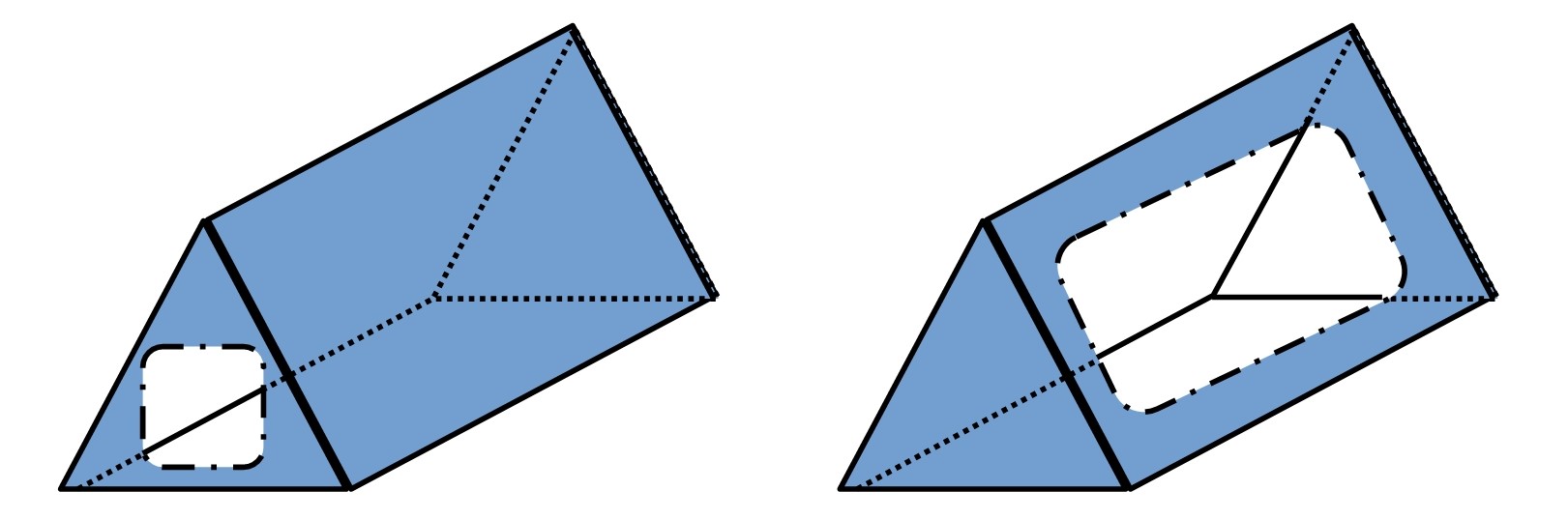
Draw Schlegel diagrams for each of these situations and some more polyhedra of your choice.  
Check that the relationship you found between V, R and E still holds for these situations. 

Extension

Draw a Schlegel diagram for a cube with an indent in one face (like the one below).  It might be easiest to imagine cutting open the face opposite the indent.  

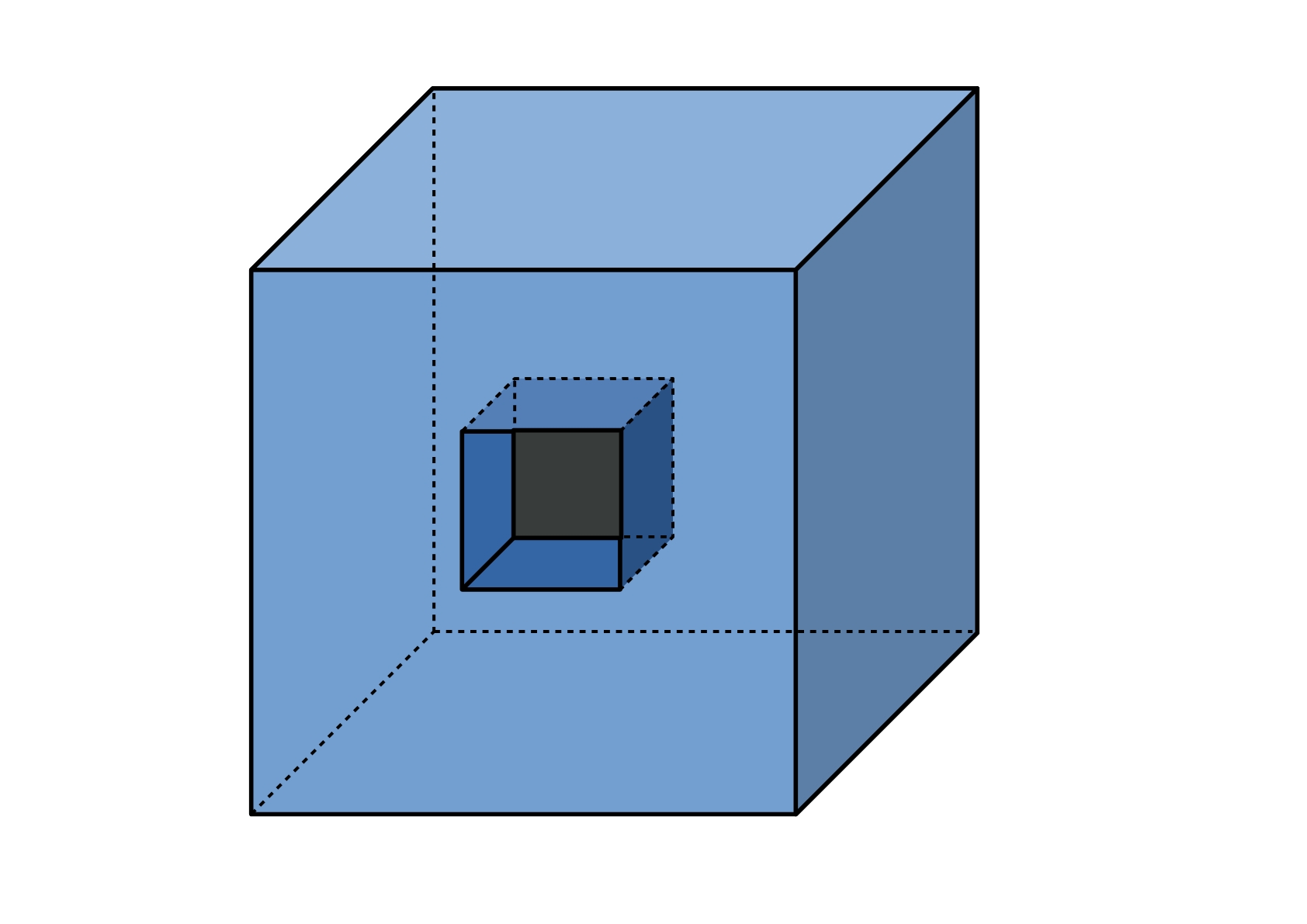
Can you explain why you do not get the same relationship between V, E and R?