Euler Meets Schlegel

Well done to Duncan from Wilson's School in England who sent in this solution.

Consider an existing connected planar network. Adding another [region] onto existing vertices would involve one less vertex added than edges created. The original shape is not disrupted. One more region is created.

An unconnected extension, consisting of a vertex at the end of an edge, will create no new regions.

Therefore, new regions that are connected to the old regions arise out of the difference between vertices and edges.

However, the first and second regions cannot build upon existing regions - they are new. The first region would be the surrounding area, and the second a shape made of equal numbers of vertices and edges. So, the first two regions can be established with no difference between vertices and edges.

The equation is $E-V+2=R$

In other words, by using the same number of vertices and edges, you can create two regions ('inside' and 'outside'), so $E - V + 2 = R$ when $E = V.$ After that, you can add 1 more region by adding 1 edge and 0 vertices, 2 edges and 1 vertex, 3 edges and 2 vertices and so on. Or you can add 1 edge and 1 vertex without changing the number of regions. Therefore the formula remains true as you add more vertices and edges to the network.

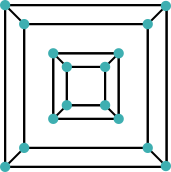
5 regions, 6 vertices, 9 edges            5 regions, 6 vertices, 9 edges

The relationship still holds true as these are connected planar shapes.

However, in a cube with an indent, the relationship does not hold as it is not connected. The indent is isolated and cannot be reached by an edge. It is like a separate network which shares the region of one face.