Where Are the Primes?
Here are some prime numbers:
$5, 17, 23, 59, 89, 101$
They are all odd. What else do they have in common?
Here are some more prime numbers:
$13, 19, 31, 37, 61, 67$
They are also all odd. What else do they have in common?
Can you find any primes greater than $3$ which are not one more, or one less, than a multiple of $6$?
Charlie thought that it wasn't possible to find any primes which were not one more, or one less than a mutiple of $6$. He thought that he might be able to use a number grid to help him prove this.
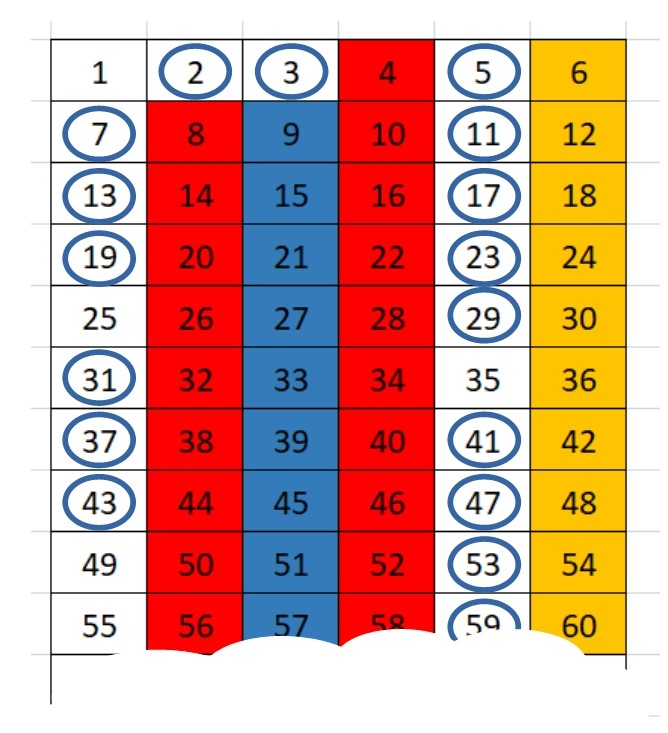
Why do you think some numbers are shaded in red, blue or yellow?
What do you notice about the numbers in circles?
Claire also though that it wasn't possible to find any primes which were not one more, or one less than a mutiple of $6$. She thought that she might be able to use some general expressions to help her prove this.
We know that $6n$ is a multiple of $6$, so cannot be prime.
We can write $6n+2=2(3n+1)$, and so we know that $6n+2$ is a multiple of $2$. The only multiple of $2$ which is prime is $2$ itself, which is not greater than $3$.
Can you complete Claire's method to show that primes numbers greater than $3$ must be of the form $6n+1$ or $6n+5$?
Can you show that you can write $6n+5$ in the form $6m-1$, and so show that numbers of the form $6n+5$ are one less than a multiple of $6$?
You may also like
Adding All Nine
Make a set of numbers that use all the digits from 1 to 9, once and once only. Add them up. The result is divisible by 9. Add each of the digits in the new number. What is their sum? Now try some other possibilities for yourself!
Doodles
Draw a 'doodle' - a closed intersecting curve drawn without taking pencil from paper. What can you prove about the intersections?