Where Are the Primes?

Jayanth from GESS in Singapore noticed what linked the prime numbers:

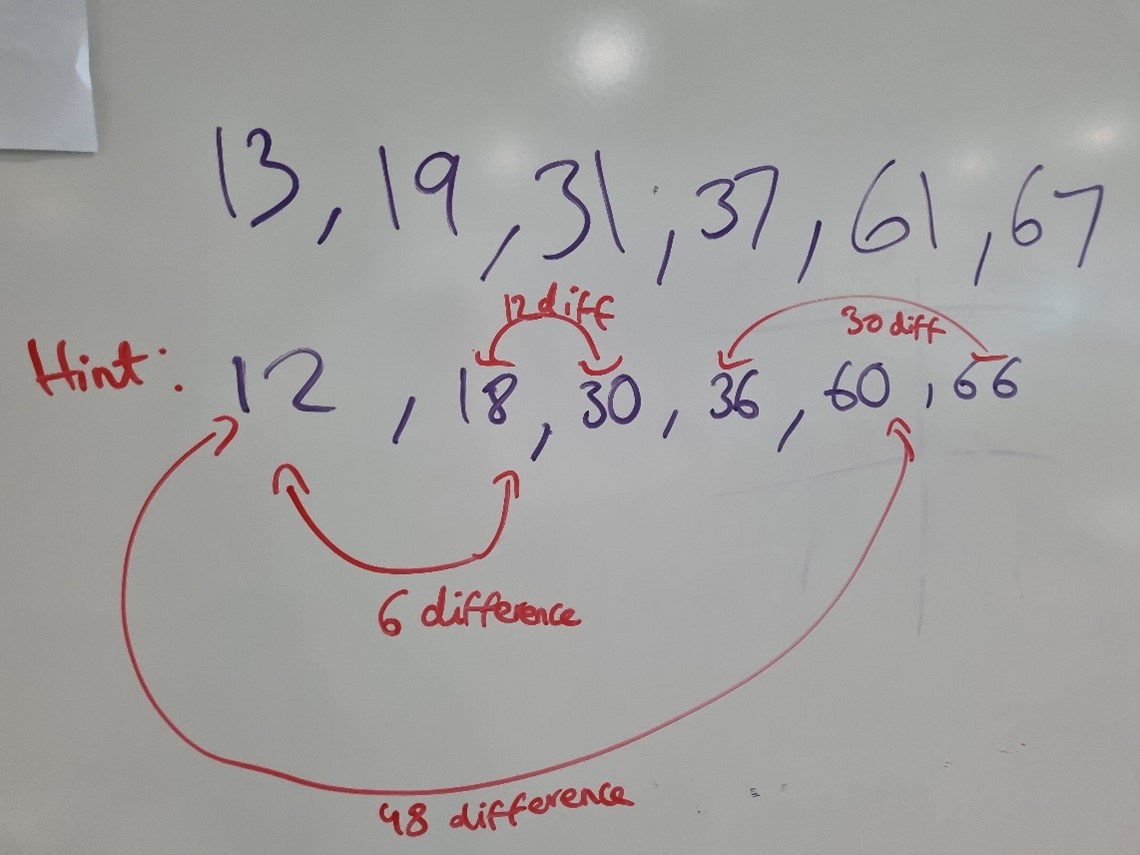
Here, the difference of any 2 numbers is a multiple of 6. In both the hint & the answer, it’s like that. 6, 12, 30 & 48 are all multiples of 6.

They all have a difference of a multiple of 6 when 2 numbers are subtracted with each other (bigger number subtracting a smaller number, not the other way around).

From comparing the two lists, you can also see that these prime numbers are all one more than a multiple of 6. The prime numbers on the first list are all one less than a multiple of 6.

Yazan from Dubai International Academy in Jordan sent in some great ideas. Yazan uses the word 'composite' to mean 'not prime'.

I don’t think there is a prime greater than 3 which is not one greater or one less than six.

Clarie’s method shows that. For example 13 is a prime number, however, it is $6n+1,$ which means it is one greater than a multiple of six, and 103 is also prime, however it is $6n+5,$ or $6n-1,$ which means it is one less than a multiple of six. All of the primes greater than three are like that. 

$6n+3$ is neither one greater nor one less than a multiple of six, but it is a multiple of 3, so they’re composite, except for three which is prime (factors of 3: 1 and 3 only), but we are looking than primes greater than 3.

To conclude, I couldn’t find a prime greater than 3 which is neither one more or one less than a multiple of six.

Sunhari from British School Muscat completed Claire's proof. Sunhari uses $|$ to mean 'is a multiple of' (for example, $3|6$ is another way of writing '3 is a multiple of 6').

$6n+1$ cannot be factorised further, and is therefore a prime.
Note here that $6n+1$ doesn't have to be a prime - for example, if $n=4$
$6n+3 = 3(2n+1)$
Therefore $3|6n+3,$ and $6n+3$ is composite.
$6n+4 = 2(3n+2)$
Therefore $2|6n+4$ and $6n+4$ is composite. 
$6n+5$ cannot be factorised, and is therefore a prime. 
Note again that $6n+5$ can be prime but doesn't have to be prime - for example, if $n=5$

Suppose $a = 6n+5$
$a + 6 = 6n+5+6$
$a+6 = 6n +6 +5$
$a+6 = 6(n+1) +5$
$a+6 = 6m +5 for $m = n+1$
$a = 6m +5-6$
$a= 6m-1$

Therefore, all primes over 3 can be written as one less or one more than a multiple of 6. (Since any numbers that are not one less or one more than a multiple of 6 are composite.)