To Swim or to Run?

Well done to Mahdi from Mahatma Gandhi International School in India who sent in this thorough solution:

Swimming Speed: 1

Running Speed: $k$

Radius of pool: $1$

(i) Case 1 (swim directly to B) is covered in this diagram when $\theta = 0$

(iii) Case 3 is covered in this diagram when $\theta = \pi$
 

Running Distance: arc AX which has length $\dfrac{\theta}{2\pi}\times 2\pi r = \theta r$

Running Time: $\dfrac{\theta r}k$ because the running speed is $k$

Swimming Distance: Chord $\text{XB}$ which has length $\text{2XM.}$ $\angle\text{XOM}=90-\frac{\theta}2$

Why $90-\frac{\theta}2$? $\angle\text{BOX}$ and $\theta$ lie on a straight line. $\angle\text{BOX}$ is in an isosceles triangle with $\angle\text{OBX}$ and $\angle\text{OXB,}$ therefore $\angle\text{OBX}$ and $\angle\text{OXB} = \angle\text{OXM}$ are both equal to $\dfrac{\theta}2.$ Triangle $\text{OMX}$ is right-angled at $\text{M.}$

$$\begin{align}\sin{\left(90-\frac{\theta}2\right)}&=\frac{\text{XM}}{\text{OX}}\\ \text{XM}&=r\cos{\left(\frac \theta 2 \right)}\\ \text{XB} &= 2r\cos{\left(\frac \theta 2 \right)}\end{align}$$

Swimming Time: $\dfrac{2r\cos{\left(\dfrac \theta 2 \right)}}1 = 2r\cos{\left(\dfrac \theta 2 \right)}$

So, total time, $T$ = Running Time + Swimming Time $$ T = \dfrac{\theta r}k + 2r\cos{\left(\dfrac \theta 2 \right)}$$

To find the minimum time, $\dfrac{\text d T}{\text d \theta}=0$ and $\dfrac{\text d^2 T}{\text d \theta^2}\gt0$ $$\begin{align}\dfrac{\text d T}{\text d \theta}&=\frac r k - 2r\sin{\left(\frac\theta2\right)}\times\frac12\\ &=r\left[\frac1k-\sin{\left(\frac\theta2\right)}\right]\end{align}$$

Now the double derivative has to be positive for there to be a minimum $$\begin{align}\dfrac{\text d^2 T}{\text d \theta^2} &= r\left[0-\cos{\left(\frac\theta2\right)}\times\frac12\right]\\ &=\frac{-r}2\cos{\left(\frac\theta2\right)}\end{align}$$

For $0\le\theta\le\pi,$ $\cos{\left(\frac\theta2\right)}\ge0$ and so $\dfrac{\text d^2 T}{\text d \theta^2}\le0$ which implies there is no minimum time between $0\le\theta\le\pi.$ Hence, the minimum is at either of the end points. There are two cases for that, as shown in the two graphs below. $r,$ the radius of pool, just adds vertical stretch.

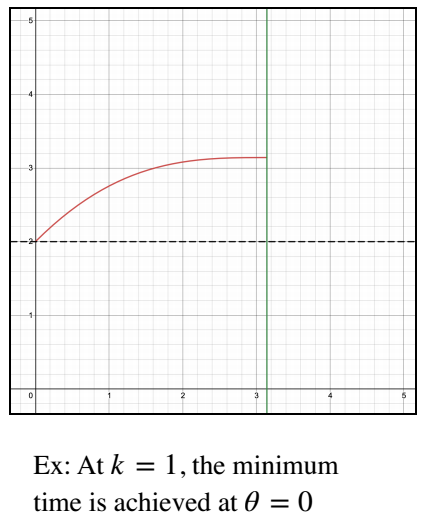
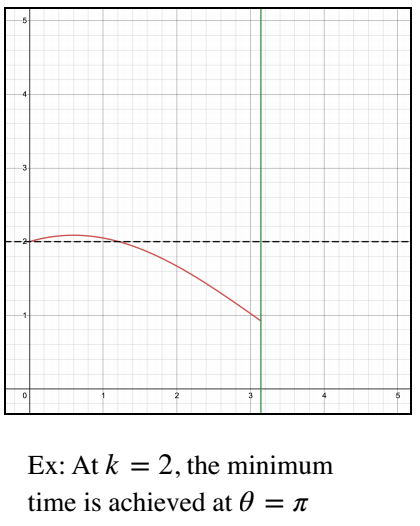
There is a value of $k$ for which the time taken at $\theta = 0$ is equal to the time taken at $\theta = \pi.$ And the time taken is $2$ for both [times $r$]. Let $r=1$ since it just adds vertical stretch to the graph.

For this value of $k,$ running all the way ($\theta = \pi$) takes time $2$ (the same amount of time that swimming all the way takes). $$2=\frac{\theta}{k}+2r\cos{\left(\frac{\theta}2\right)}\\ 2=\frac{\pi}{k}+2r\cos{\left(\frac{\pi}2\right)} \\ 2=\frac{\pi}{k}$$ So we get $k = \dfrac \pi2$. We can thus conclude that:

For $0\lt\theta\lt\dfrac\pi2,$ the minimum time is achieved at $\theta = 0.$ So option (i) swim directly.

For $\dfrac\pi2\lt\theta\lt\pi,$ the minimum time is achieved at $\theta = \pi.$ So option (iii) run around.