Circumference Angles

Circumference Angles printable sheet - proof sorter
Circumference Angles printable sheet - corollaries

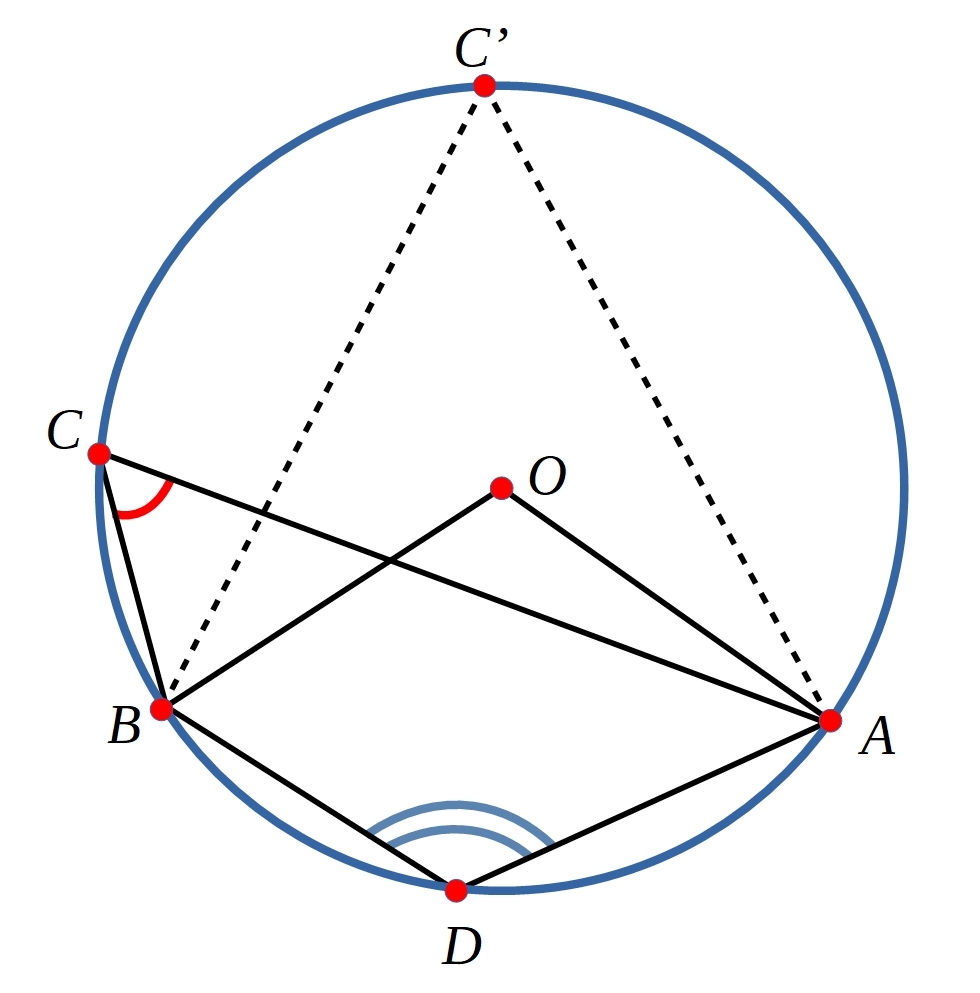
Try moving the points $A$, $B$ and $C$ around (but keep them in the order $A, B, C$ going clockwise!). 

What do you notice about the two angles marked in the diagram?  

Can you use the diagram below to prove your findings?

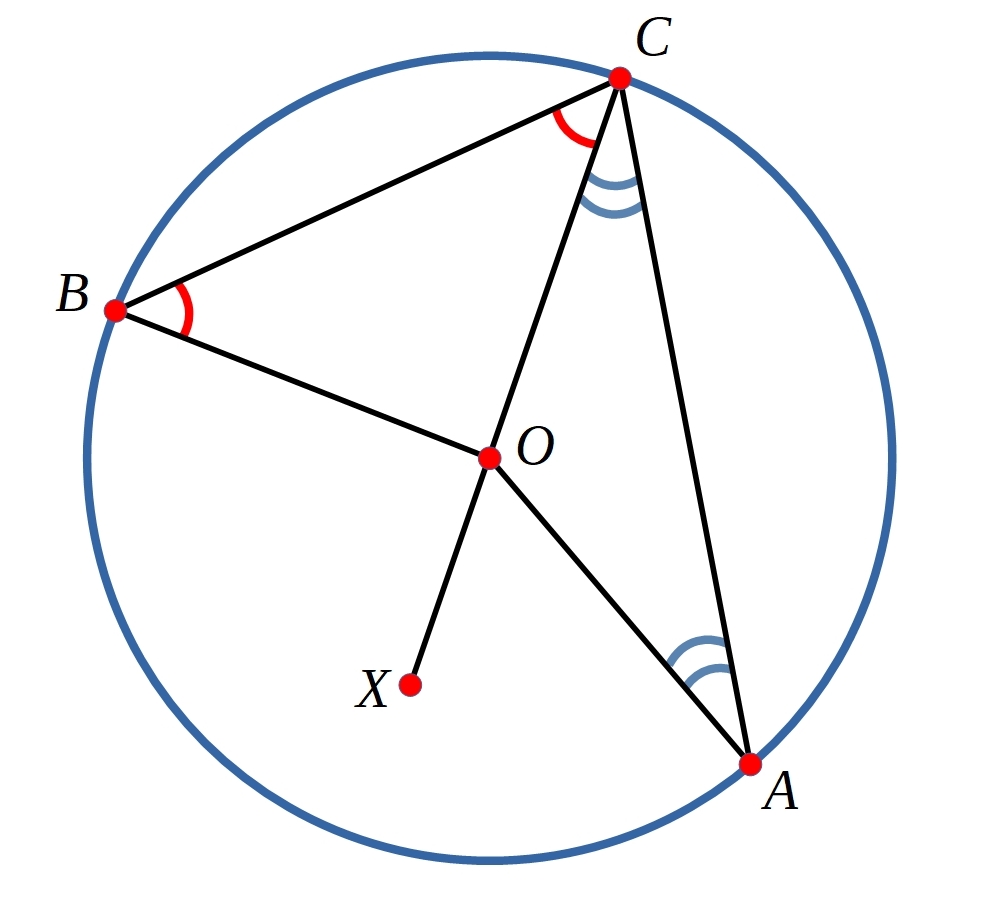
You might like to use this Proof Sorter to help you construct a proof.

Having now proved this result, you can use it to show that some other things are also true. 
Propositions which follow on from a theorem are sometimes called corollaries.

Corollary 1

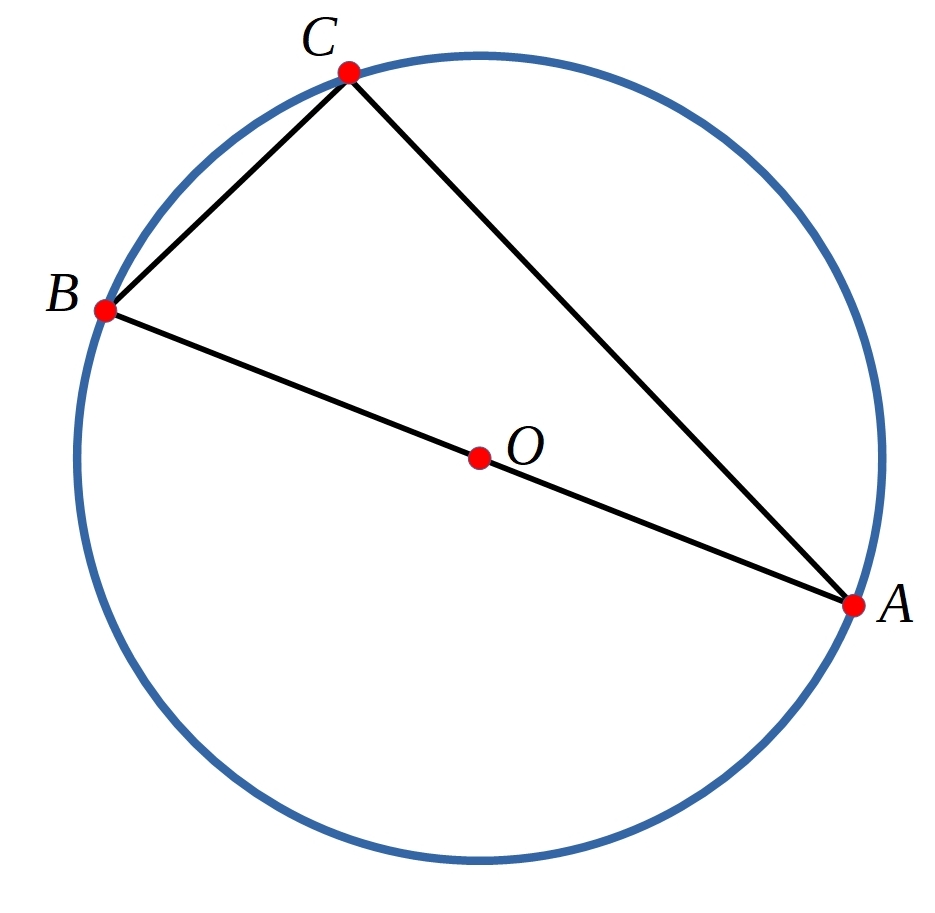
Can you show that the angle in a semi-circle is a right-angle?
(I.e. if $AB$ is a diameter then angle $ACB=90^{\circ}$.)
 

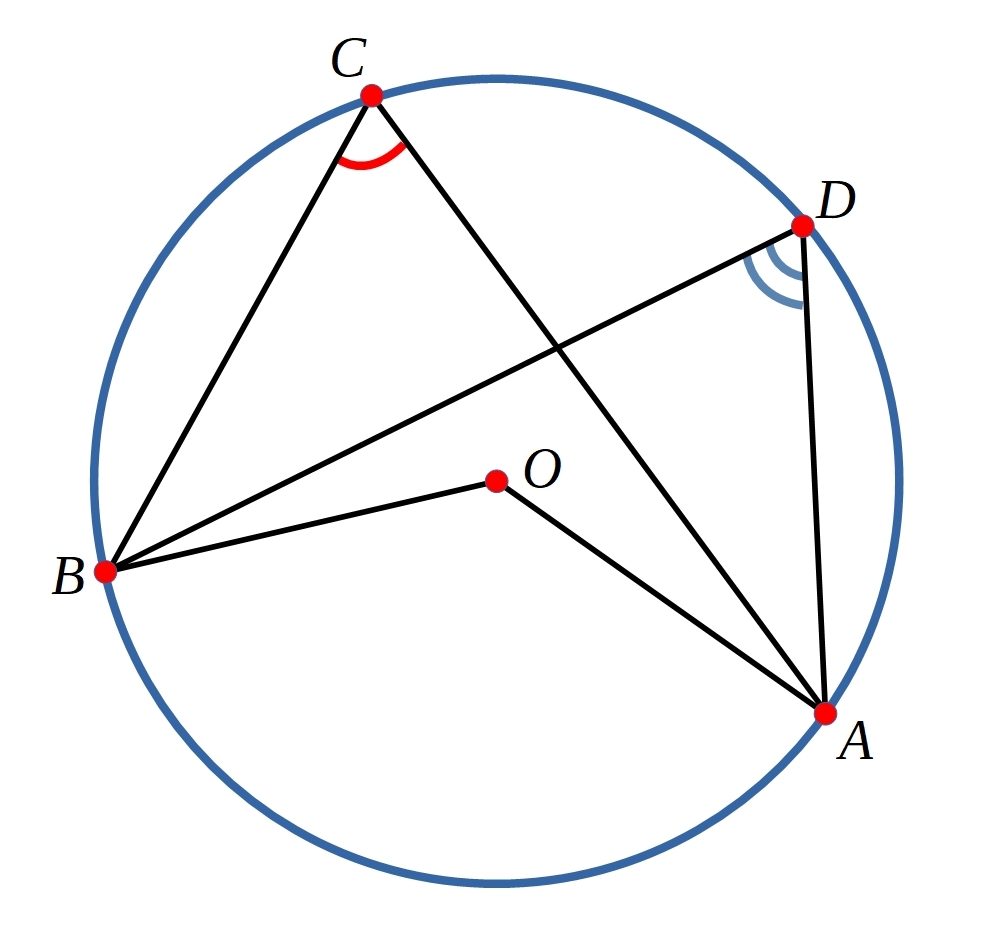
Corollary 2

Can you show that the two angles marked in the diagram below are equal?

Corollary 3

Can you show that the two angles marked in the diagram below add up to $180^{\circ}$?

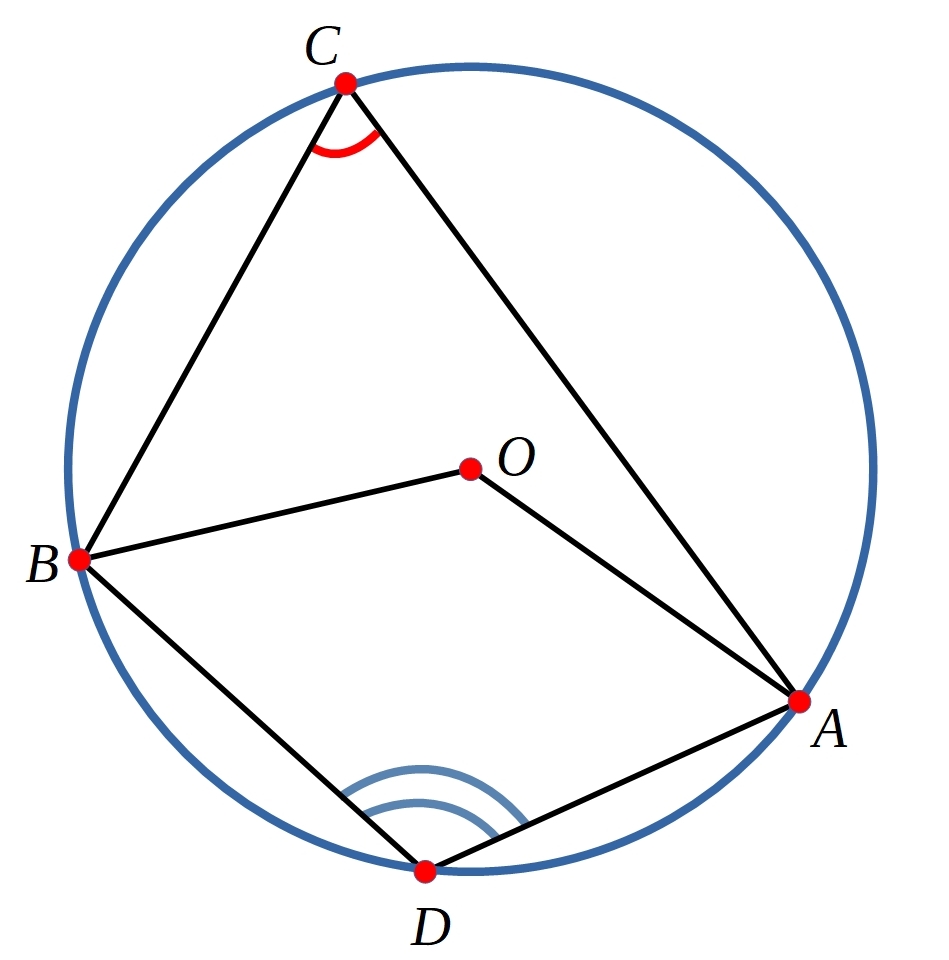
Can you use your results to show that the two angles marked in the diagram below add up to $180^{\circ}$?