Circumference Angles

Well done to Ci Hui Minh Ngoc Ong from Kong Hwa School in Singapore, Nayanika from The Tiffin Girls' School and Lewis from Wilson's School, both in the UK, who sent in complete proofs for the original problem.

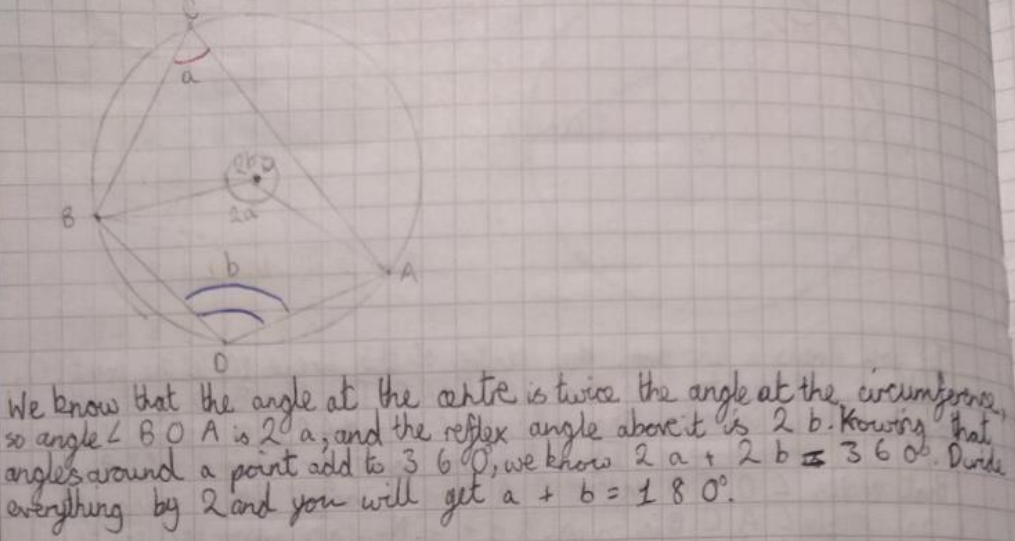
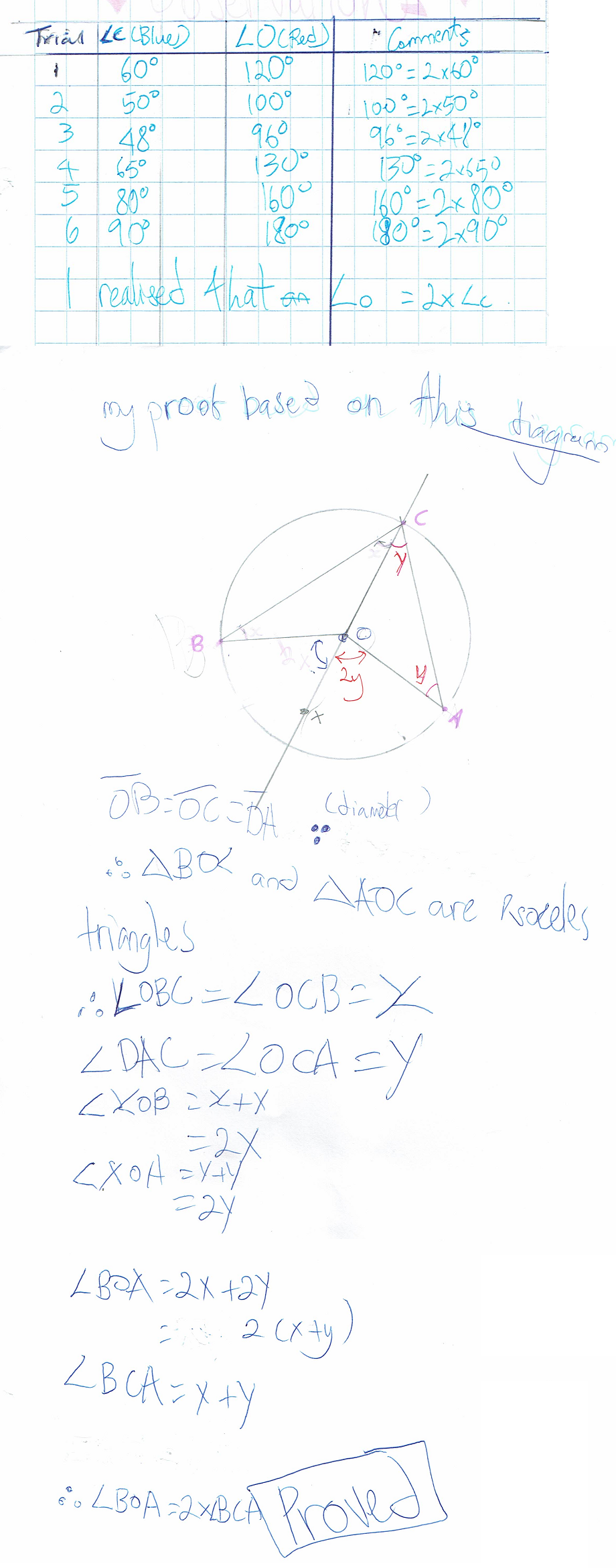
This is Ci Hui Minh Ngoc Ong's work for the original problem:

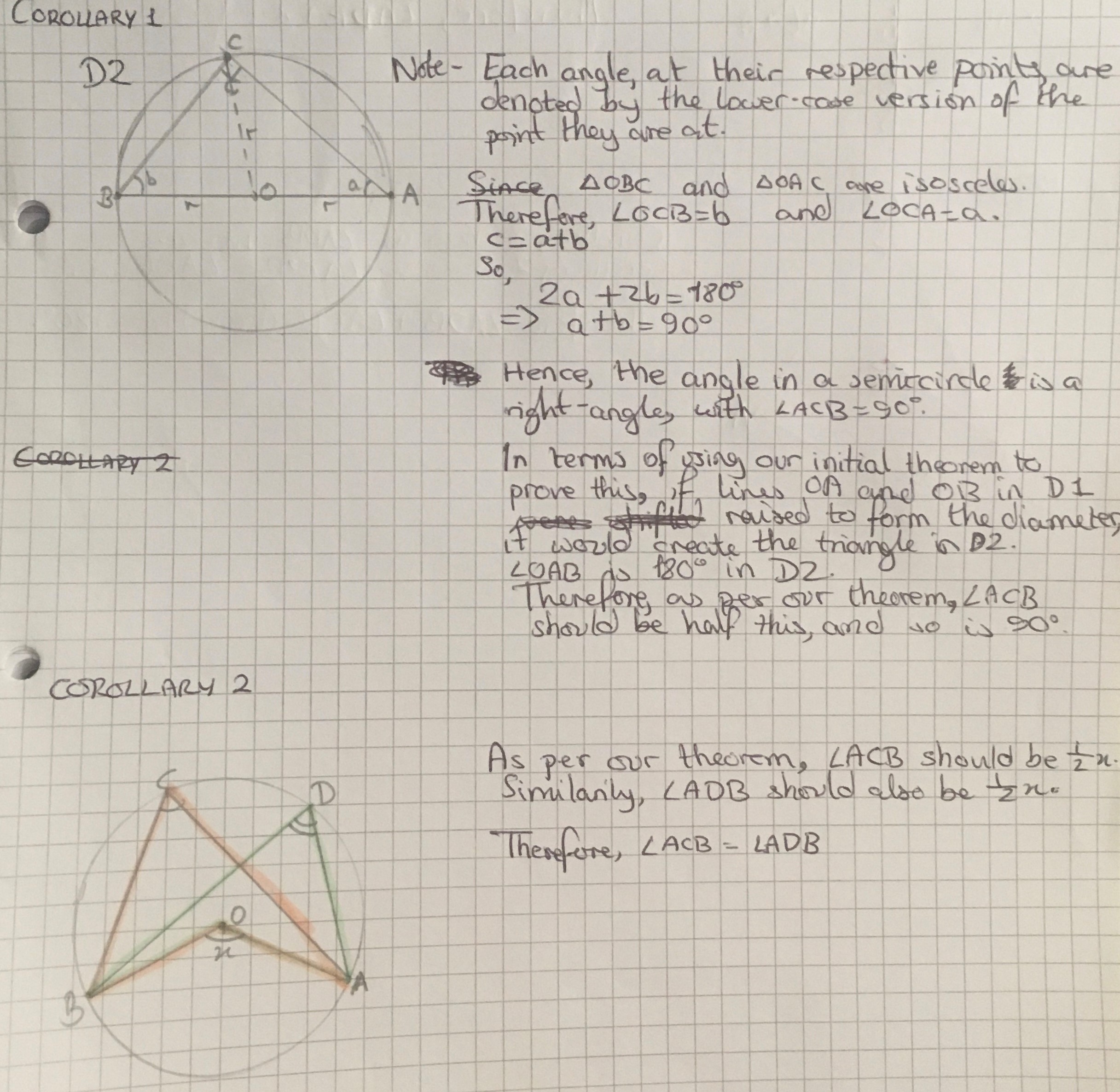
Harry from Crestwood Community School, Lewis and Nayanika sent in proofs for corollaries 1, 2 and 3. This is Nayanika's work for corollaries 1 and 2 (click on the image to see a larger version):

Harry proved corollary 2 in a slightly different way. Harry wrote:

Both D and C are connected to A and B, D and C can be moved freely without the angle changing, meaning that they are both the same angle because they are both connected to the same points.

Here is Lewis's proof of corollary 3 (click to see a larger version):

Nayanika and Lewis also proved corollary 4. Here is Nayanika's work (click to see a larger version):