Tetra Slice

Thatcher from Rugby School in the UK, Farhan from King Edward VI Camp Hill Boys in England, Ci Hui Minh Ngoc Ong from Kelvin Grove State College (Brisbane) in Australia and Thanh Delta Global School in Vietnam from used similar triangles to show that PQRS is a parallelogram. Thatcher introduces the idea in this beautiful video, which makes excellent use of GeoGebra.

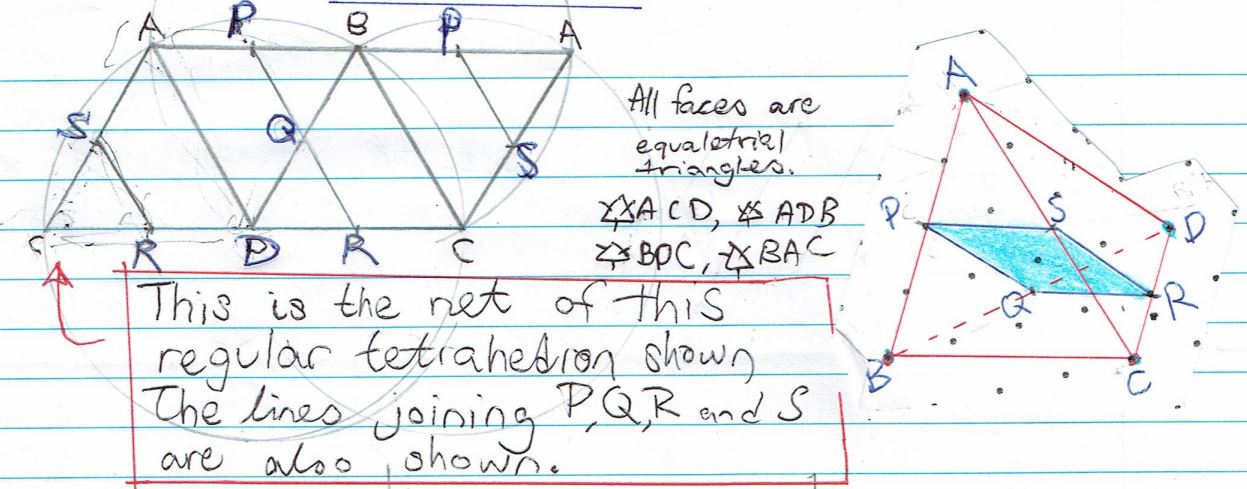
This is Farhan's proof, illustrated with Ci Hui Minh Ngoc's diagrams, including a picture of the net of the tetrahedon (in this case a regular tetrahedron is shown).

As $P$ and $S$ are the midpoints of $AB$ and $AC$ respectively, the ratio $\dfrac{AP}{AB} = \dfrac{AS}{AC} = \frac12.$
This, along with the fact that triangles $ABC$ and $APS$ share angle $BAC$ is sufficient to say that $APS$ and $ABC$ are similar triangles, so we can conclude that $PS$ is parallel to $BC.$
Similar logic in triangle $BCS$ allows us to conclude that $QR$ is also parallel to $BC,$ and therefore $PS$ is parallel to $QR.$
Repeating the argument with the other 2 faces tells us that the remaining sides are also parallel to each other, so $PQRS$ is a parallelogram.

(You can use a similar technique to prove that the quadrilateral formed by joining all 4 midpoints of any quadrilateral is also a parallelogram)

Dylan from Brooke Weston and Joshua from Bohunt Sixth Form, both in the UK, used vectors to show that PQRS is a parallelogram. They both used position vectors relative to the 'origin'. This is Dylan's work (click to englarge):

For the case of the regular tetrahedron, Dylan used vectors to show that PQRS is a rhombus (Dylan claims that it is a square, but so far we do not have evidence of right angles):

Farhan and Ci Hui Ming Ngoc Ong and Thanh used similar triangles to show PQRS is a rhombus, and explained why a square. Here is Farhan's work:

If the tetrahedron is regular and of side $s$, the similar triangles show us that $PQ = QR = RS = PS = 0.5s.$ So $PQRS$ is a rhombus. By symmetry we can see that all angles of the rhombus must be equal, so we in fact have a square.

Thanh proved that PQRS is a square by considering perpendicular bisectors: