What We Do and Why We Do It

The following informs the work of NRICH

Beliefs and culture

These beliefs inform the work we do:

• All students have the right to shine and all have the right to struggle
• A person's mathematical ability is not fixed: everyone can make progress
• Learning is a messy business, which often involves taking wrong turns and making mistakes
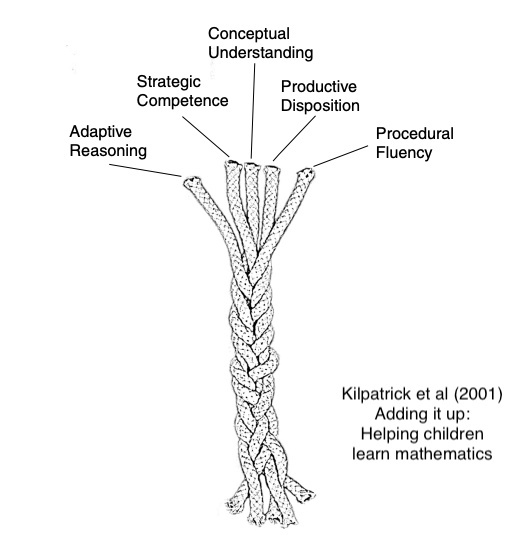
• Working mathematically requires more than just conceptual understanding and procedural fluency; it also requires the ability to reason, to think strategically and to have a productive disposition (Kilpatrick et al p115)

For those who would like to dig a little deeper into our beliefs, take a look at What We Think and Why We Think It.

Task design

We design rich tasks which encourage all students to work and think mathematically:

• Our low threshold high ceiling tasks offer accessible starting points and a selection of extension opportunities
• HOTS not MOTS: Tasks requiring Higher Order Thinking Skills replace More of the Same
• Tasks nurture students' natural curiosity about mathematics
• We offer students the opportunity to go on mathematical journeys:
  Exploring -> Noticing patterns -> Conjecturing -> Generalising -> Justifying -> Proving

Role of the teacher and student

The structure of our tasks influences the nature of classroom interactions: 

• Alan Wigley's model for teaching mathematics recommends starting with a challenge, or problem to be explored, and then building on students' ideas
• If students are to develop resilience ("I can't do this... YET"), it is important for teachers to signal to students that they can all make progress (Wheeler, page 5 bullet points)
• Our tasks offer teachers opportunities for supporting students in a way that still expects students to do the important mathematical thinking

An example of what this might look like in practice can be found here.

Multiple strategies

Resourceful mathematicians appreciate that there is not just one way to approach a problem:

• We publish students' solutions to our tasks, rather than just answers, to draw attention to the range of possible ways in which students have tackled our problems
• Students appreciating the connections between multiple representations (numeric, diagrammatic and algebraic) strengthens their understanding
• Our tasks are structured in a way that encourages teachers to offer students opportunities for discussion and the sharing of ideas