What we think and why we think it

The development of NRICH resources is informed by the following beliefs:

Natural Curiosity

• All of us are naturally curious about mathematics.
• It is intrinsically satisfying to gain mathematical understanding.
• There are many ways of working mathematically.
  
  Thinking Mathematically
   
• Mathematics is a worthwhile, interesting and engaging activity in its own right.
• Truth in mathematics is established by deductive reasoning rather than empirical evidence or opinion.
• Mathematics has order and structure and can be beautiful.
  
  Working Collaboratively
  
• Exchanging questions and ideas is an important part of working mathematically.
• We learn by reflecting on our mistakes and misconceptions.
  
  Growth Mindset and Determination
   
• Mathematical ability is not fixed: everyone can make progress.
• Everyone should have the opportunity to grapple with problems that they do not yet know how to solve.
• Eveyone should have the opportunity to succeed mathematically.
   

This leads us to believe that all learners are entitled to:

• a rich mathematical learning experience
• assessment criteria that offer them opportunities to succeed
• a challenging mathematical curriculum which offers them opportunities to struggle

NRICH aims to offer free resources for teachers who are committed to nurturing curious, confident, resourceful and enthusiastic learners of mathematics. To find out more, see What We Do and Why We Do It.
 

Our beliefs are informed by articles, books, videos and research. 
Here is a selection which may interest you.

Natural Curiosity

Models for Teaching Mathematics (with permission from ATM)
Alan Wigley invites us to take a closer look at the curriculum we offer to learners of mathematics. He questions whether it is the job of the teacher to make it easy for students.

Mathematical Etudes
This article by Colin Foster presents the idea of mathematical etudes as a way to develop fluency without tedium.

Why Play I Spy When You Can Do Mathematics? (with permission from ATM)
Robert Andrews and Paul Andrews have some conversations about mathematics.

Angle Measurement: an Opportunity for Equity
Paul Andrews attempts to establish a principle of worthwhile mathematical activity for all pupils. 

Tasks Promoting Inquiry
A video of a talk Dan Meyer gave to a group of teachers in Cambridge.


Thinking Mathematically

The Role of the Teacher by David Wheeler

Relational Understanding and Instrumental Understanding 
Richard Skemp draws attention to the need to teach for relational understanding (whereby students know what to do and are able to explain why) rather than instrumental understanding (whereby students know rules and procedures without understanding why they work).

Three linked articles by Dave Hewitt: 
Arbitrary and Necessary Part 1: A Way of Viewing the Mathematics Curriculum
Arbitrary and Necessary Part 2: Assisting Memory
Arbitrary and Necessary Part 3: Educating Awareness

Effective Teachers of Numeracy: Report of a study carried out for the Teacher Training Agency by Askew, M. et al

Train Spotters' Paradise (with permission from ATM)
Dave Hewitt alerts us to 'the richness that can be gained by looking at a particular situation in some depth, rather than looking at it superficially in order to get a result for a table and then rushing on to the next example'.

An Exploratory Approach to Advanced Mathematics
Kenneth Ruthven outlines a three-part approach to the teaching and learning of mathematics (exploration, codification, consolidation).

Learning and Doing Mathematics by John Mason

Thinking Mathematically by John Mason, Leone Burton and Kaye Stacey

Primary Questions and Prompts for Mathematical Thinking by Margaret Jeffcoat, Margaret Jones, Jill Mansergh, John Mason, Heather Sewell and Anne Watson

Mathematics is beautiful (no, really) 
Vicky Neale encourages us to offer students the opportunity to engage with rich questions, play with mathematical ideas, and experience multiple strategies to the same question rather than just getting the answer in the back of the textbook and moving on.

Mathematics as human activity: a different handshakes problem by Tim Rowland


Working Collaboratively

Complex Instruction - Raising Achievement Through Group Worthy Tasks
Jo Boaler's research on the benefits of collaborative work in the classroom including a video clip of students working collaboratively.

Improving Reasoning: Analysing Alternative Approaches
Malcolm Swan describes a teaching approach designed to improve the quality of students' reasoning.

Mindset and Determination

Boosting Achievement with Messages that Motivate 
Carol Dweck draws attention to fixed and growth mindsets, and what we do as teachers to reinforce them.

The power of believing that you can improve - TED Talk by Carol Dweck

Horizon: Fermat's Last Theorem
In this film mathematician Andrew Wiles talks about his personal experience of seeking a proof of Fermat's Last Theorem. 

James Nottingham's work on the 'learning pit' in which you create cognitive conflict or cognitive 'wobble' for learners to grapple with, which encourages deeper thinking and a sense of achievement when a solution is reached

How Children Fail by John Holt
In particular, the section "October 1, 1959" where John Holt describes seeing Dr Gattegno teach a group of students. (p156-163 in 1990 edition. Extract also available online, see pages 94-98 of this pdf.)

Learning Without Limits by Susan Hart, Annabelle Dixon, Mary Jane Drummond and Donald McIntyre



General Reading

I could be the best mathematician in the world... if I actually enjoyed it Part 1 and Part 2 by Elena Nardi and Susan Steward (with permission from ATM) 

Is Mathematics T.I.R.E.D.? A Profile of Quiet Disaffection in the Secondary Mathematics Classroom by Elena Nardi and Susan Steward (full PDF available upon request)

The Improving Attainment in Mathematics Project, run by Anne Watson, Els De Geest and Stephanie Prestage

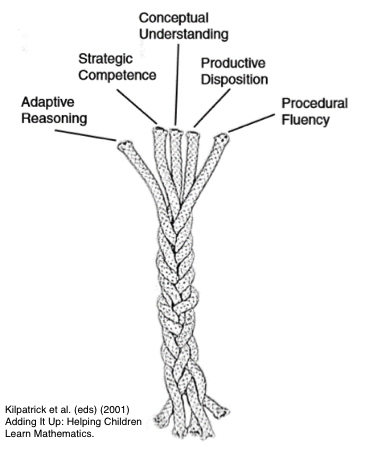
Strands of Mathematical Proficiency, chapter 4 from Adding It Up: Helping Children Learn Mathematics by Kilpatrick et al.

Mindset: How you can fulfil your potential by Carol S Dweck

Building Learning Power by Guy Claxton

Youcubed - Project co-founded by Jo Boaler at Stanford University, with resources and articles supporting growth mindsets and effective teaching

Habits of Mind: an organizing principle for mathematics curriculum by Al Cuoco, E. Paul Goldenberg & June Mark

Approaches to learning and teaching Mathematics by members of the NRICH team