The Koch Snowflake

The Koch Snowflake is made by repeating the following process.

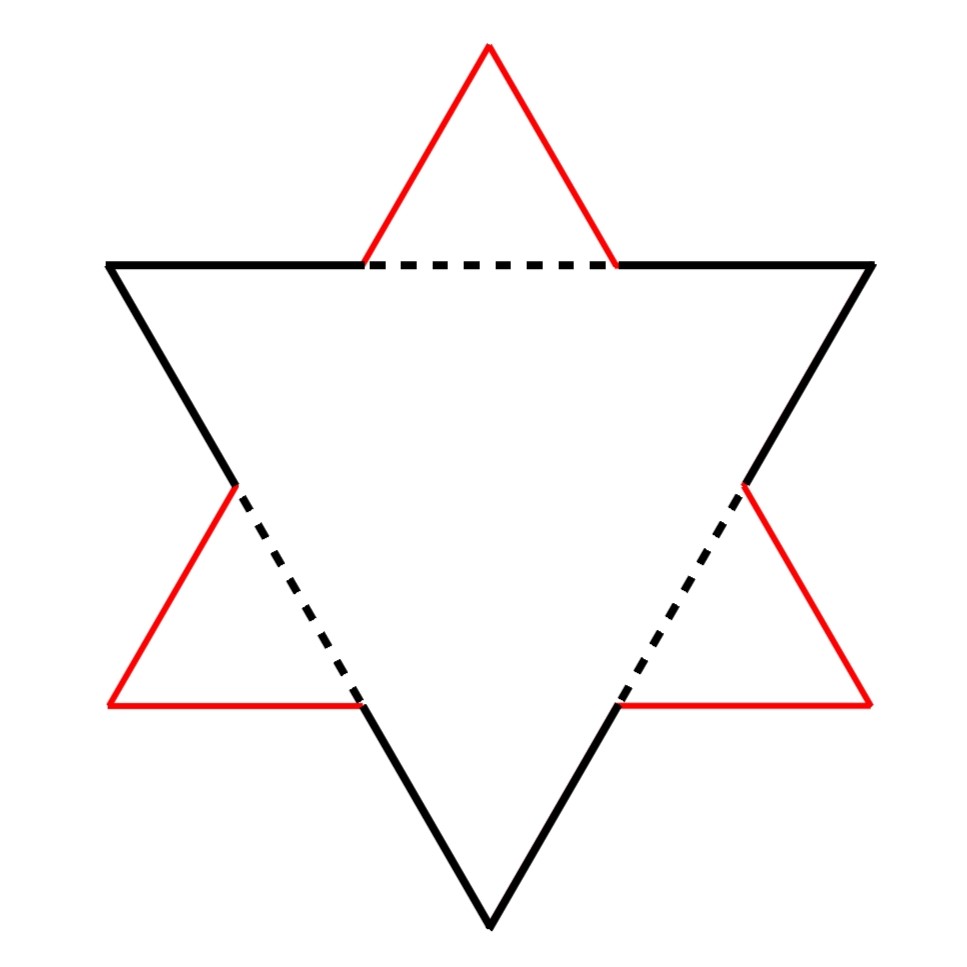
Start with an equilateral triangle.  Split each side into three equal parts, and replace the middle third of each side with the other two sides of an equilateral triangle constructed on this part.  The diagram below shows this step, with the original equilateral triangle in black, and the middle third of each side (the dotted part) being replaced with two red sides.

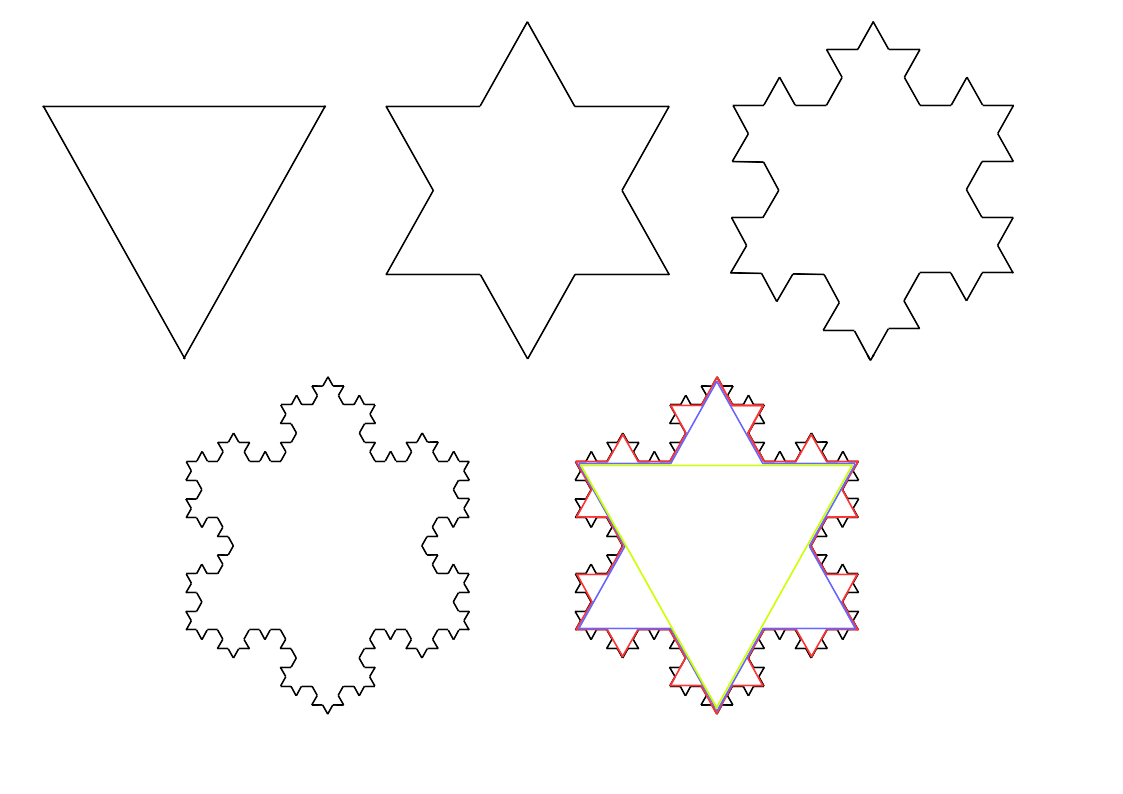
This process is then repeated, with each straight edge being split into three and the middle third at each stage being replaced by the other two sides of an equilateral triangle constructed on this section of the line. The diagram below shows the first 4 shapes in the process, as well as a picture showing all four superimposed on each other. 

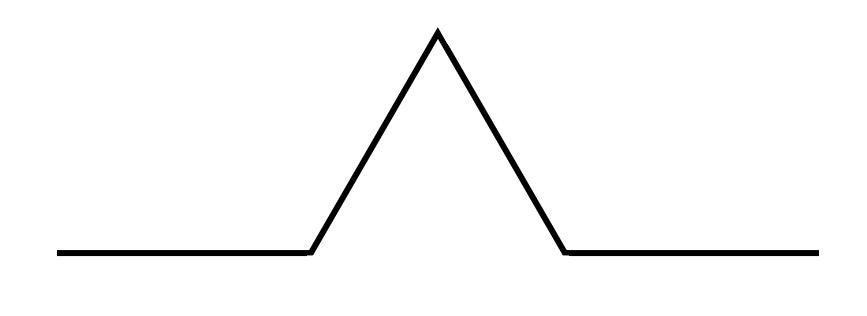
A different way of thinking about this process is to notice that at each stage every straight line is replaced by a line that looks like this:

The Koch Snowflake Curve is the shape you get if you continue this process forever.  The video below shows the first six stages of the infinite process for generating the Koch snowflake.

Here are some questions about the Koch Snowflake.

1. There are three edges in the first iteration of the snowflake.  How many edges are there in the second iteration?  How many in the third iteration?
2. Find a formula for the total number of edges of the $n^{\text {th}}$ iteration.
3. If the first iteration has edges of length 1, how long are the edges in iteration 2?
4. Find a formula for the length of each edge in the $n^{\text {th}}$ iteration.
5. Use your results to find a formula for the total length of the $n^{\text{th}}$ iteration of the snowflake.  What happens to the length of the snowflake as $n$ gets larger?

Now consider the area of the Koch Snowflake.

1. Let the area of the first iteration be $A$ (you might be able to actually calculate $A$ given that you know the lengths of the edges).  What is the extra area added on by each extra triangle in the second iteration?
   This diagram might help!  Remember that the original triangle has area $A$.
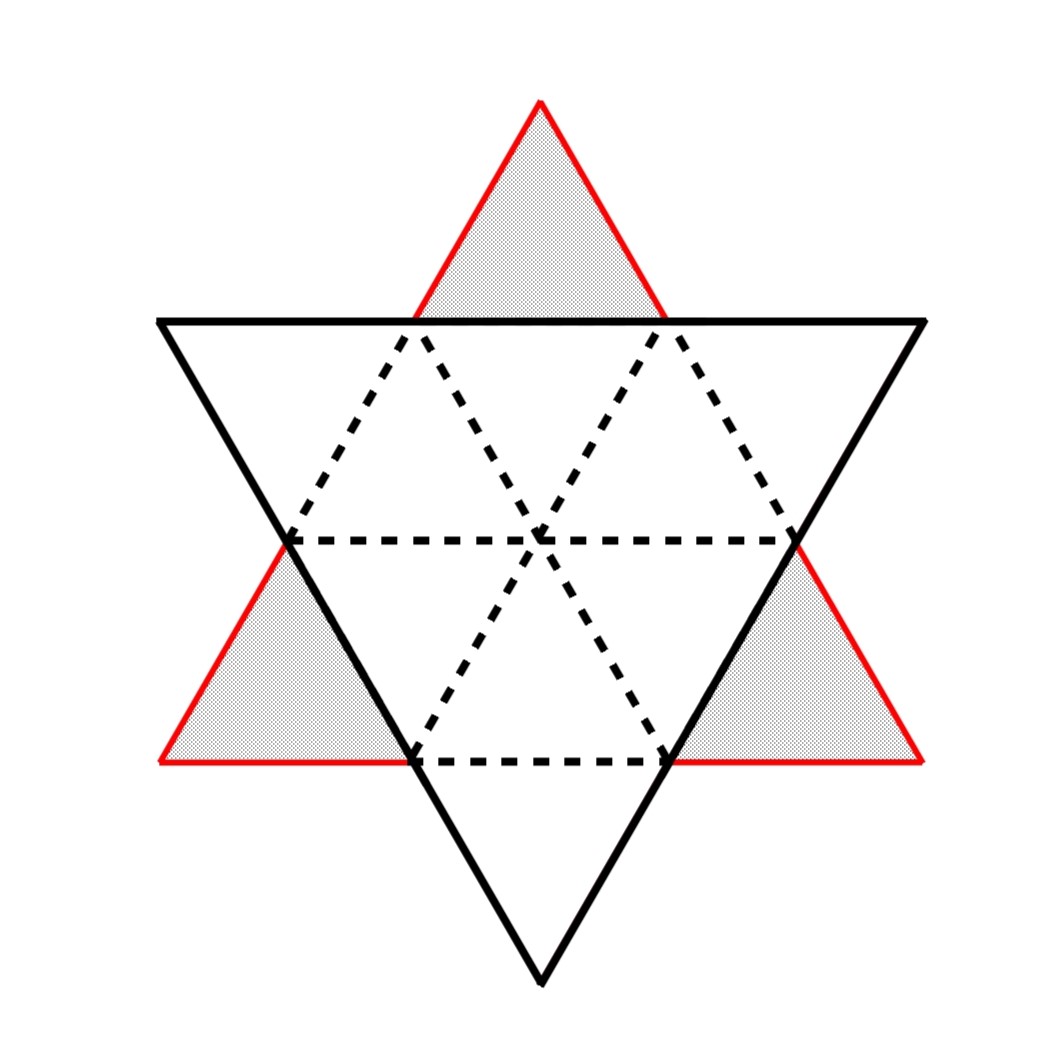
2. How much area in total is added by the second iteration?
3. How much area is added by the third iteration?
4. Can you find an infinite sum for the area of the Koch Snowflake?  Can you simplify this?
   It might be easier to work out separately the size of each extra triangle at each stage and also the number of triangles added each time.  The can then be combined to give the extra area added each time.

 How do the length and the area behave as the number of sides increase?