The Koch Snowflake

Maria, Malaika and Elliot from London Academy of Excellence Tottenham (LAET) in the UK explored the side lengths and total perimeter for the first few iterations of the snowflake. Here is Maria's work:

Thatcher from Rugby School UK and China, Prasangi from Bronx High School of Science in New York, Yash from Tanglin Trust School in Singapore, Nishad from Thomas Estley Community College, William from Simon Balle All-through School in the UK, Ci Hui Minh Ngoc Ong from Kelvin Grove State College (Brisbane) in Austrialia, Emily from Bishop's Wordsworth's Grammar School in the UK and Samuel, Kawthar and Kim from LAET used a formula to investigate the perimeter. Here is Samuel's work:

Nishad simplified the formula and commented on what happens in the long term:

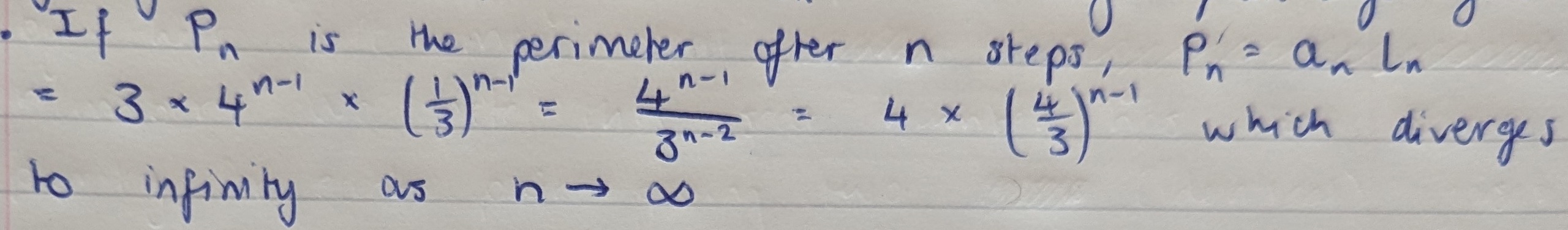
Prasangi, Maria, Malaika, Elliot, Thatcher, Yash, Nishad, William, Ci Hui Minh Ngoc Ong, Emily, Samuel, Kawthar and Kim also investigated the areas of the triangles. This is William's explanation of the areas of the triangles added in the first two iterations (click to enlarge):

Prasangi, Thatcher, Nishad, William and Ci Hui Minh Ngoc Ong continued in this way to find the total area of each iteration. This is Nishad's work:

Yash, Emily, Samuel, Kawthar and Kim did the same, but used numbers rather than $A$ for the areas. This is Emily's work:

Thatcher compiled their work into a full paper. Click here to see Thatcher's work.

Ci Hui Ming Ngoc Ong put the formulas for the side lengths and areas into a spreadsheet to calculate them automatically (click on the image to see more rows):

Ci Hui Minh Ngoc Ong then used the spreadsheet to create graphs showing how the side lengths, perimeter, small triangle area and total area change with more iterations: