Skip over navigation
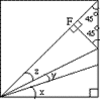
Andrei Lazanu proved the double angle formulae illustrated in the diagram:
The diagram starts from a right angled triangle, of sides $2t$ and 2 and where consequently $\tan\theta = t$. In this triangle, a line making an angle $\theta$ with the hypotenuse is drawn. This way, an isosceles triangle is formed, and $2\theta$ is the angle exterior to this isosceles triangle. Let the sides DA and DB of this isosceles triangle be $x$\ units. Then the length of DC must be $2-x$ units. Using Pythagoras' Theorem for triangle ADC we find $x$. $$x^2=(2t)^2+(2-x)^2.$$ Hence $x=1+t^2$ and so the length of side DC is $2-(1+t^2)=1-t^2$.
The formulae for the sine, cosine and tangent of $2\theta$ in terms of $t$, where $t=\tan \theta$, follow directly from the ratios of the sides of the right angled triangle ADC and we get $$\tan2\theta = {2t\over {1-t^2}},\quad \sin2\theta = {2t\over {1+t^2}},\quad \cos2\theta = {{1-t^2}\over {1+t^2}}$$
$$T= \left( \begin{array}{cc} cos 2(\phi-\theta) & -sin2(\phi-\theta)\\ sin2(\phi-\theta & \cos2(\phi-\theta) \end{array} \right) $$
Reflect Again
Age 16 to 18
Challenge Level 
Andrei Lazanu proved the double angle formulae illustrated in the diagram:
The diagram starts from a right angled triangle, of sides $2t$ and 2 and where consequently $\tan\theta = t$. In this triangle, a line making an angle $\theta$ with the hypotenuse is drawn. This way, an isosceles triangle is formed, and $2\theta$ is the angle exterior to this isosceles triangle. Let the sides DA and DB of this isosceles triangle be $x$\ units. Then the length of DC must be $2-x$ units. Using Pythagoras' Theorem for triangle ADC we find $x$. $$x^2=(2t)^2+(2-x)^2.$$ Hence $x=1+t^2$ and so the length of side DC is $2-(1+t^2)=1-t^2$.
The formulae for the sine, cosine and tangent of $2\theta$ in terms of $t$, where $t=\tan \theta$, follow directly from the ratios of the sides of the right angled triangle ADC and we get $$\tan2\theta = {2t\over {1-t^2}},\quad \sin2\theta = {2t\over {1+t^2}},\quad \cos2\theta = {{1-t^2}\over {1+t^2}}$$
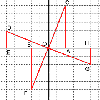
Rots and Refs provides a proof of the translation formula
.
Finally, to find the combined transformation you have to
multiply the transformation matricies to get (using the double
angle formulae to simplify):
$$T= \left( \begin{array}{cc} cos 2(\phi-\theta) & -sin2(\phi-\theta)\\ sin2(\phi-\theta & \cos2(\phi-\theta) \end{array} \right) $$
Which is a rotation. If the angles are equal the matrix would
be:
$$T= \left( \begin{array}{cc} 1 & 0\\ 0 & 1
\end{array} \right) $$
So the two reflections combined would leave all points unchanged.
You may also like
8 Methods for Three by One
This problem in geometry has been solved in no less than EIGHT ways by a pair of students. How would you solve it? How many of their solutions can you follow? How are they the same or different? Which do you like best?
Rots and Refs
Follow hints using a little coordinate geometry, plane geometry and trig to see how matrices are used to work on transformations of the plane.
Flipping Twisty Matrices
Investigate the transformations of the plane given by the 2 by 2 matrices with entries taking all combinations of values 0, -1 and +1.