Skip over navigation
Well done Robert of Madras College, St Andrew's, Scotland and Andrei of School No. 205, Bucharest, Romania for your solutions to this problem.
In both parts of this question we consider the limiting case of a process which is repeated infinitely often and things are not what they might seem to be.
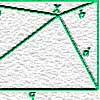
(a) In a square $ABCD$ with sides of length 1 unit a path is drawn from $A$ to the opposite corner $C$ so that all the steps in the path are either parallel to $AB$ or parallel to $BC$ and not necessarily equal steps. If we draw paths of this sort putting in more and more and more steps the length of the path is
always the same."
The steps parallel to $AB$ together must stretch all the way across from $A$ to $B$ and the steps parallel to $BC$ together must stretch all the way up from $A$ to $D$. Irrespective of the number of small steps, A point moving on any path of this type moves a total of 1 unit parallel to $AB$ and a total of one unit parallel to $BC$, hence a total of 2 units altogether. With more and more steps the path gets closer and closer to the diagonal so you might expect the length to converge to $\sqrt 2$. Surprisingly the length is always 2 units and not even close to $\sqrt 2$ units.
(b) Now consider the graphs of $y={1\over 2^n}\sin 2^nx$ for $n= 1,2,3, ...$ and $0\leq x \leq 2\pi$. As $n$\ tends to infinity the graphs oscillate more and more and get closer and closer to the $x$ axis. We have to prove that the length of the curve from $x=0$ to $x=2 \pi$ is the same for all values of $n$. The hint says we don't need to calculate the length of the path here and we should think about scale factors.
The graph of $G_n:\ y={1\over 2^n}\sin 2^nx$ from $x=0$ to $x=\pi$ is similar to the graph of $G_{n-1}:\ y={1\over 2^{n-1}}\sin 2^{n-1}x$ from $x=0$ to $x=2\pi$\ but scaled down by a linear scale factor of 1/2 so $G_n$ is half the length of $G_{n-1}$. However $G_n$ is repeated twice periodically between $x=0$ and $x=2\pi$ so the two pieces together have the same length as $G_{n-1}$.
This shows that all these graphs on $0\leq x \leq 2\pi$ have the same length although as $n\rightarrow \infty$ the graphs get closer and closer to the $x$ axis so you might suppose that the length converges to $2\pi$. Surprisingly the length is always the same and much more than $2\pi$.
Small Steps
Age 16 to 18
Challenge Level 
Well done Robert of Madras College, St Andrew's, Scotland and Andrei of School No. 205, Bucharest, Romania for your solutions to this problem.
In both parts of this question we consider the limiting case of a process which is repeated infinitely often and things are not what they might seem to be.
(a) In a square $ABCD$ with sides of length 1 unit a path is drawn from $A$ to the opposite corner $C$ so that all the steps in the path are either parallel to $AB$ or parallel to $BC$ and not necessarily equal steps. If we draw paths of this sort putting in more and more and more steps the length of the path is
always the same."
The steps parallel to $AB$ together must stretch all the way across from $A$ to $B$ and the steps parallel to $BC$ together must stretch all the way up from $A$ to $D$. Irrespective of the number of small steps, A point moving on any path of this type moves a total of 1 unit parallel to $AB$ and a total of one unit parallel to $BC$, hence a total of 2 units altogether. With more and more steps the path gets closer and closer to the diagonal so you might expect the length to converge to $\sqrt 2$. Surprisingly the length is always 2 units and not even close to $\sqrt 2$ units.
(b) Now consider the graphs of $y={1\over 2^n}\sin 2^nx$ for $n= 1,2,3, ...$ and $0\leq x \leq 2\pi$. As $n$\ tends to infinity the graphs oscillate more and more and get closer and closer to the $x$ axis. We have to prove that the length of the curve from $x=0$ to $x=2 \pi$ is the same for all values of $n$. The hint says we don't need to calculate the length of the path here and we should think about scale factors.
The graph of $G_n:\ y={1\over 2^n}\sin 2^nx$ from $x=0$ to $x=\pi$ is similar to the graph of $G_{n-1}:\ y={1\over 2^{n-1}}\sin 2^{n-1}x$ from $x=0$ to $x=2\pi$\ but scaled down by a linear scale factor of 1/2 so $G_n$ is half the length of $G_{n-1}$. However $G_n$ is repeated twice periodically between $x=0$ and $x=2\pi$ so the two pieces together have the same length as $G_{n-1}$.
This shows that all these graphs on $0\leq x \leq 2\pi$ have the same length although as $n\rightarrow \infty$ the graphs get closer and closer to the $x$ axis so you might suppose that the length converges to $2\pi$. Surprisingly the length is always the same and much more than $2\pi$.
You may also like
Climbing Powers
$2\wedge 3\wedge 4$ could be $(2^3)^4$ or $2^{(3^4)}$. Does it make any difference? For both definitions, which is bigger: $r\wedge r\wedge r\wedge r\dots$ where the powers of $r$ go on for ever, or $(r^r)^r$, where $r$ is $\sqrt{2}$?
Little and Large
A point moves around inside a rectangle. What are the least and the greatest values of the sum of the squares of the distances from the vertices?
Approximating Pi
By inscribing a circle in a square and then a square in a circle find an approximation to pi. By using a hexagon, can you improve on the approximation?