Skip over navigation
Hexy-metry
Age 14 to 16
Challenge Level 
 |
A hexagon is inscribed inside a circle.
The sides of the hexagon are alternately $a$ and $b$ units in length.
What is the radius of the circle?
|
You may also like
Bendy Quad
Four rods are hinged at their ends to form a convex quadrilateral. Investigate the different shapes that the quadrilateral can take. Be patient this problem may be slow to load.
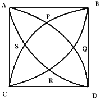
Quadarc
Given a square ABCD of sides 10 cm, and using the corners as centres, construct four quadrants with radius 10 cm each inside the square. The four arcs intersect at P, Q, R and S. Find the area enclosed by PQRS.
Get Cross
A white cross is placed symmetrically in a red disc with the central square of side length sqrt 2 and the arms of the cross of length 1 unit. What is the area of the disc still showing?