Skip over navigation
Quadarc
Age 14 to 16
Challenge Level 
Given a square $ABCD$ of sides $10$ cm, and using the corners as centres, construct four quadrants with radius $10$ cm each inside the square. The four arcs intersect at $P$, $Q$, $R$ and $S$. Find the area enclosed by $PQRS$.
You may also like
Bendy Quad
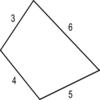
Four rods are hinged at their ends to form a convex quadrilateral. Investigate the different shapes that the quadrilateral can take. Be patient this problem may be slow to load.
Get Cross
A white cross is placed symmetrically in a red disc with the central square of side length sqrt 2 and the arms of the cross of length 1 unit. What is the area of the disc still showing?
