Skip over navigation
Here is a hint to help on you on the way :
Let $\alpha + \beta = \gamma$ and $\tan(\alpha + \beta) = \frac{\tan\alpha + \tan\beta}{1 - \tan\alpha\tan\beta}$
where $\alpha = \tan^{-1}{1\over3}$, $\beta = \tan^{-1}{1\over2}$, $\gamma = \tan^{-1}1$.
Three by One
Age 16 to 18
Challenge Level 
Here is a hint to help on you on the way :
Let $\alpha + \beta = \gamma$ and $\tan(\alpha + \beta) = \frac{\tan\alpha + \tan\beta}{1 - \tan\alpha\tan\beta}$
where $\alpha = \tan^{-1}{1\over3}$, $\beta = \tan^{-1}{1\over2}$, $\gamma = \tan^{-1}1$.
You may also like
Flexi Quads
A quadrilateral changes shape with the edge lengths constant. Show the scalar product of the diagonals is constant. If the diagonals are perpendicular in one position are they always perpendicular?
Tetra Perp
Show that the edges $AD$ and $BC$ of a tetrahedron $ABCD$ are mutually perpendicular if and only if $AB^2 +CD^2 = AC^2+BD^2$. This problem uses the scalar product of two vectors.
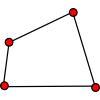
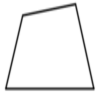
Flexi Quad Tan
As a quadrilateral Q is deformed (keeping the edge lengths constnt) the diagonals and the angle X between them change. Prove that the area of Q is proportional to tanX.