Skip over navigation
We had over 100 new submissions for this popular challenge. First from Orchards School in Wisbech, Cedar Class
Amelia says, “8 and 120 are not the number because 8 is one digit and 120 has 3 digits.”
Aironas then adds, “It can't be 18 or 83 because they have odd digits.”
“46 and 22 don't have a tens number greater than the units number, so it can't be them,” suggests Matas.
Jessica states, “86 is not it because it has 6 in it (the 3x) and the rest are not.”
Tommy D says, “It isn't 42 because the tens digit is double the ones digit.”
There are now only 2 possible answers left: 64 and 80.
Lastly, Tommy C goes for it! “I think 64 is the answer because 6 + 4 = 10 and 10 is in the 5 times table.”
Cedar Class have also made their own Number Detective challenges!
You are welcome to try them”¦Their document can be viewed hereCedar Class Wisbech.docx
From the same school but from Hawthorn Class (Year 3), Colleen sent in the following:
The answer is 64 as we worked it out by using the steps and crossing off any answers which didn't meet the criteria.
The answer is not:
• 120 and 8 as they do not have two digits. 120 have three digits and 8 has one digit.
• 83 and 18 did not have two even numbers
• In 22 tens and units are equal. In 46 the ones are greater than the tens.
• In 86 the 6 is a multiple of 3
• In 42 double the 2 is 4
• In 80 the sum of the digits is 8 which is not a multiple of 5
Isabel from Clyst Heath Primary School sent in the following:
I read the clues first and decided to start with the last clue because that would eliminate most of the numbers - The sum of the two digits is a multiple of 5. That left me with 64/46. Then I searched for a clue that would allow me to cancel out one without easily. I chose the clue, The tens digit is bigger than the units digit, that allowed me to cancel out 46
leaving me with 64 and thats my answer.
Jacob from St. John's Primary sent in a picture of his work.
Shivoham from Robin Hood Junior School also sent in a picture showing the working out.
From Westridge School for Girls in the USA these three Sandhya, Salvia and Saba sent in good solutions.
I recommend that you view larger versions here.
Sandhya.JPG
Salvia.JPG
Saba.JPG
Thank you all so much for these excellent solutions and sharing how you found the answer.
Number Detective
Age 5 to 11
Challenge Level 
We had over 100 new submissions for this popular challenge. First from Orchards School in Wisbech, Cedar Class
Amelia says, “8 and 120 are not the number because 8 is one digit and 120 has 3 digits.”
Aironas then adds, “It can't be 18 or 83 because they have odd digits.”
“46 and 22 don't have a tens number greater than the units number, so it can't be them,” suggests Matas.
Jessica states, “86 is not it because it has 6 in it (the 3x) and the rest are not.”
Tommy D says, “It isn't 42 because the tens digit is double the ones digit.”
There are now only 2 possible answers left: 64 and 80.
Lastly, Tommy C goes for it! “I think 64 is the answer because 6 + 4 = 10 and 10 is in the 5 times table.”
Cedar Class have also made their own Number Detective challenges!
You are welcome to try them”¦Their document can be viewed hereCedar Class Wisbech.docx
From the same school but from Hawthorn Class (Year 3), Colleen sent in the following:
The answer is 64 as we worked it out by using the steps and crossing off any answers which didn't meet the criteria.
The answer is not:
• 120 and 8 as they do not have two digits. 120 have three digits and 8 has one digit.
• 83 and 18 did not have two even numbers
• In 22 tens and units are equal. In 46 the ones are greater than the tens.
• In 86 the 6 is a multiple of 3
• In 42 double the 2 is 4
• In 80 the sum of the digits is 8 which is not a multiple of 5
Isabel from Clyst Heath Primary School sent in the following:
I read the clues first and decided to start with the last clue because that would eliminate most of the numbers - The sum of the two digits is a multiple of 5. That left me with 64/46. Then I searched for a clue that would allow me to cancel out one without easily. I chose the clue, The tens digit is bigger than the units digit, that allowed me to cancel out 46
leaving me with 64 and thats my answer.
Jacob from St. John's Primary sent in a picture of his work.
Shivoham from Robin Hood Junior School also sent in a picture showing the working out.
From Westridge School for Girls in the USA these three Sandhya, Salvia and Saba sent in good solutions.
I recommend that you view larger versions here.
Sandhya.JPG
Salvia.JPG
Saba.JPG
Thank you all so much for these excellent solutions and sharing how you found the answer.
You may also like
Number Round Up
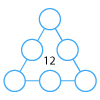
Arrange the numbers 1 to 6 in each set of circles below. The sum of each side of the triangle should equal the number in its centre.
Grouping Goodies
Pat counts her sweets in different groups and both times she has some left over. How many sweets could she have had?
Prime Magic
Place the numbers 1, 2, 3,..., 9 one on each square of a 3 by 3 grid so that all the rows and columns add up to a prime number. How many different solutions can you find?