Lots of Lollies
If you are a teacher, click here for a version of the problem suitable for classroom use, together with supporting materials. Otherwise, read on ...
Frances and Rishi were given a bag of lollies.
They shared them out equally and had one left over.
Just as they had finished sharing them their friends Kishan, Hayley and Paul came along. They wanted some lollies too so the children shared them out again between all of them. This time they had two lollies left over.
How many lollies could there have been in the bag?
Once you've had a chance to think about it, click below to see how three different groups of pupils began working on the task.
Sarah, Danielle and Sally said:
We also notice that $7$ works and $27$ works, as well as $107$."
Poppy began like this:
If the two children end up with one lolly it must be an odd number of lollies. Then three more children come making the total number of children $5$. Say they had $1$ lolly each when they shared them, the number of lollies would be $7$ because $1$ times $5$ is $5$ add on $2$ for the left over ones and it makes seven. If we carry this on to $10$ lollies each it shows:
$1$ lolly each - $7$ lollies
$2$ lollies each - $12$ lollies
$3$ lollies each - $17$ lollies
$4$ lollies each - $22$ lollies
$5$ lollies each - $27$ lollies
$6$ lollies each - $32$ lollies
$7$ lollies each - $37$ lollies
$8$ lollies each - $42$ lollies
$9$ lollies each - $47$ lollies
$10$ lollies each - $52$ lollies
Here is the start of Phoebe and Alice's work:
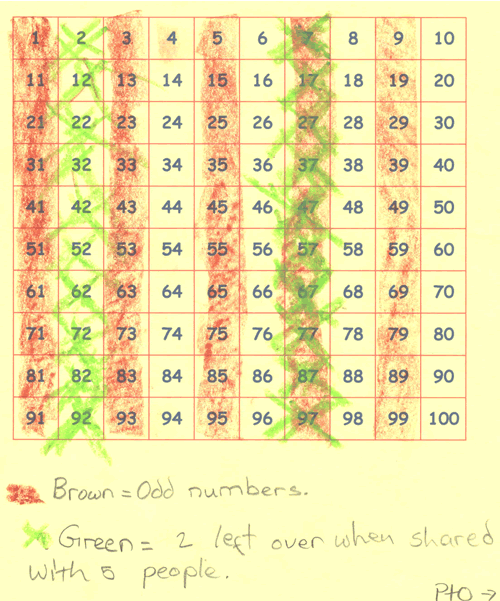
Can you take each of these starting ideas and develop it into a solution?
Can you adapt each of these strategies to find the number of lollies when there are three friends to start with and two friends join them?
How many lollies could there be in the bag if there was 1 lolly left over to start with, and then 1, 2, 3 or 4 lollies left when they were shared between the five children?
Or 2 lollies left over to start with...?
What if we started with four friends, and two more friends join them...?
You may also like
Let's Investigate Triangles
Vincent and Tara are making triangles with the class construction set. They have a pile of strips of different lengths. How many different triangles can they make?
