Skip over navigation
Congratulations Andrei, School No. 205, Bucharest, Romania on another excellent solution.
1. I observed that a cube could be represented by the diagram below, that keeps all edges and vertices (the lengths are not important).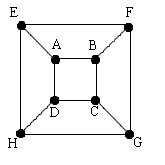
From the beginning I observe that one could start from any vertex in a cube and there are $8$ vertices.
From any vertex there are three possible routes. I shall consider the routes starting from vertex $A$.
Below are written all the possible combinations I found starting with the edge $AD$:
I observe that there are $6$ possible paths, $4$ of which are Hamiltonian Circuits.
I have to multiply the number of solutions I obtained. So the total number of solutions is given by $8 \times3 \times6$ that is $144$, and $96$ are Hamiltonian Circuits.
Because all vertices of the cube are indistinguishable, there are $18$ solutions, and $12$ Hamiltonian Circuits.
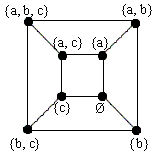
2. Set $\{a, b, c\}$ has the following subsets: $\{a, b, c\}, \{a, b\}, \{a, c\}, \{b, c\}, \{a\}, \{b\}, \{c\}, \phi $. I observe that they could be arranged so that one subset is connected with $3$ other subsets that differ from the first by only one element, deleted or inserted. These subsets can be positioned on the vertices of a cube.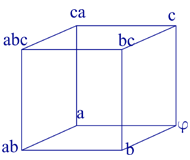


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Cube Net
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Congratulations Andrei, School No. 205, Bucharest, Romania on another excellent solution.
1. I observed that a cube could be represented by the diagram below, that keeps all edges and vertices (the lengths are not important).

From the beginning I observe that one could start from any vertex in a cube and there are $8$ vertices.
From any vertex there are three possible routes. I shall consider the routes starting from vertex $A$.
Below are written all the possible combinations I found starting with the edge $AD$:
| Path | Circuit |
| A-D-C-B-F-E-H-G | No |
| A-D-C-B-F-G-H-E-A | Yes |
| A-D-C-G-H-E-F-B-A | Yes |
| A-D-C-G-F - impossible | |
| A-D-H-E-F-B-C-G | No |
| A-D-H-E-F-G-C-B-A | Yes |
| A-D-H-G-C-B-F-E-A | Yes |
| A-D-H-G-F-E - impossible |
I observe that there are $6$ possible paths, $4$ of which are Hamiltonian Circuits.
I have to multiply the number of solutions I obtained. So the total number of solutions is given by $8 \times3 \times6$ that is $144$, and $96$ are Hamiltonian Circuits.
Because all vertices of the cube are indistinguishable, there are $18$ solutions, and $12$ Hamiltonian Circuits.
2. Set $\{a, b, c\}$ has the following subsets: $\{a, b, c\}, \{a, b\}, \{a, c\}, \{b, c\}, \{a\}, \{b\}, \{c\}, \phi $. I observe that they could be arranged so that one subset is connected with $3$ other subsets that differ from the first by only one element, deleted or inserted. These subsets can be positioned on the vertices of a cube.


I have verified that each subset is connected with $3$ other
subsets, forming a diagram as found before, or, more intuitively, a
cube. So, the problem is reduced to the first problem.
The number of sequences is $144$ sequences, or $18$ if the
first element of the sequence does not matter.
You may also like
Instant Insanity
Given the nets of 4 cubes with the faces coloured in 4 colours, build a tower so that on each vertical wall no colour is repeated, that is all 4 colours appear.
Network Trees
Explore some of the different types of network, and prove a result about network trees.
Magic Caterpillars
Label the joints and legs of these graph theory caterpillars so that the vertex sums are all equal.

