Skip over navigation
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Area L
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
We received solutions from Amrit, Adithya, Guruvignesh and Agathiyan, all from Hymers College, and Pablo from Kings College Alicante. Here is Pablo's solution:
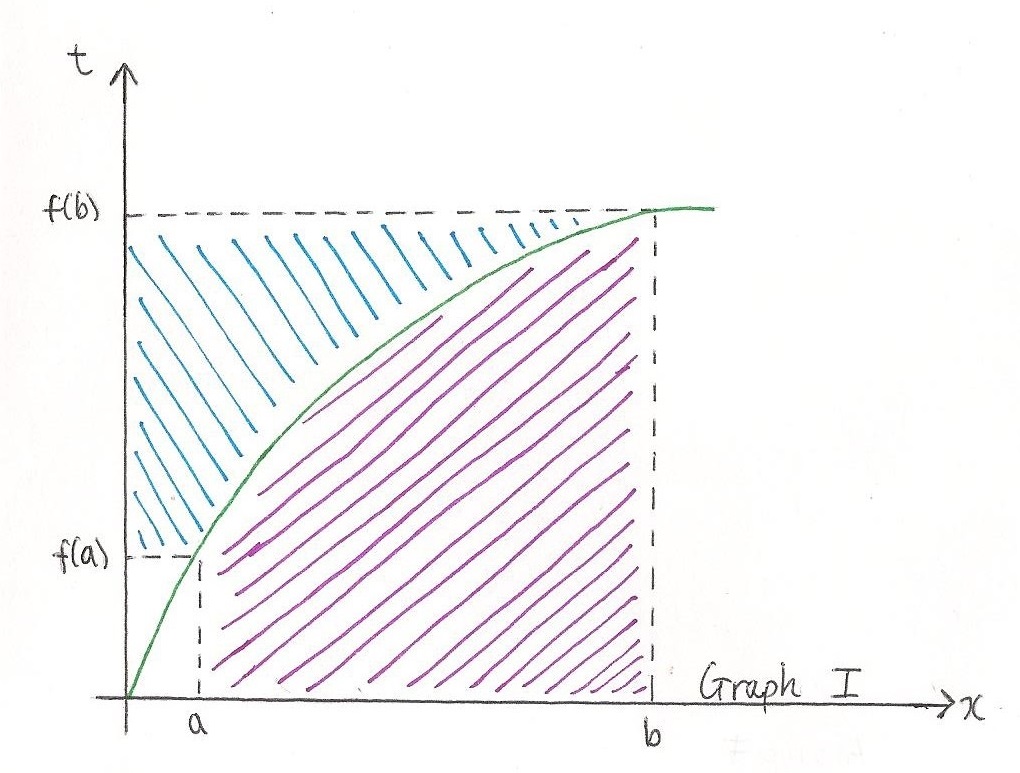
As you can see in Graph I, the areas in purple and blue add up to the big rectangle, $bf(b)$, minus $af(a)$, the small rectangle.
There is a change of variable in $f^{-1}(t)$ because the area isn't taken
from the x-axis, but from the t-axis. $f^{-1}(x)$ is the inverse of $f(x)$. It is obtained either by switching variables and rearranging the equation again or by reflecting it in the line y=x.
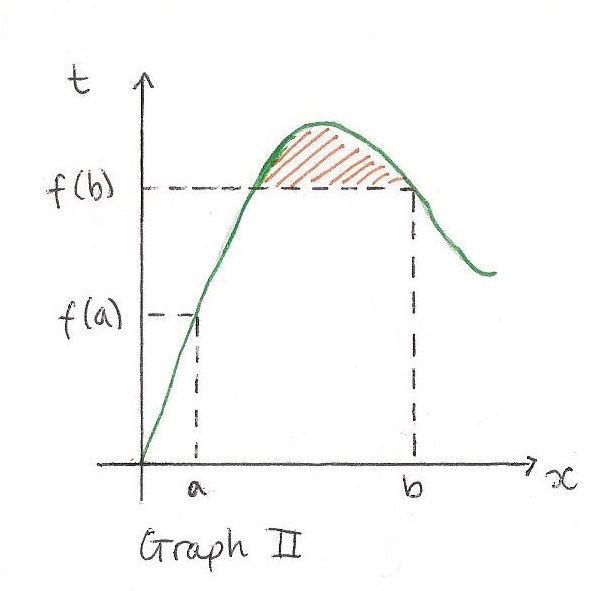
The reason why $f(x)$ must be increasing in the interval $a \leq x \leq b$ is shown in Graph II. If it weren't, if at some point it reached a turning point and began to decrease, the area (orange) at the top would not be accounted for.
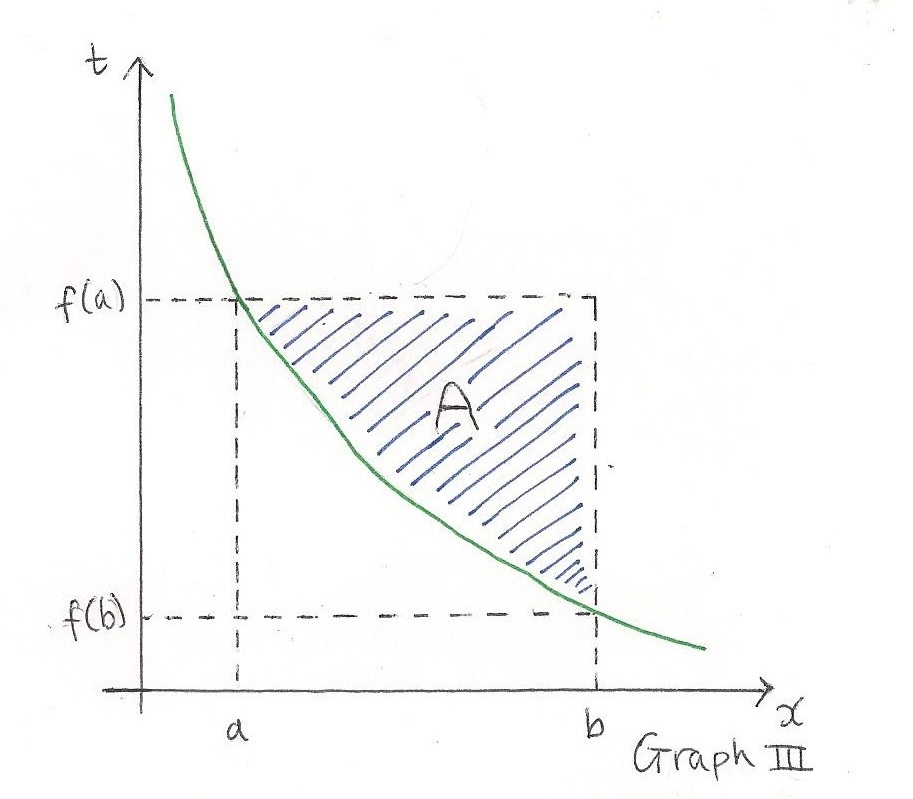
If $f(x)$ is always decreasing in the interval $a \leq x \leq b$, a similar formula comes out, but through more algebraic manipulation. The area called A in Graph III is:
$A = bf(a) - bf(b) - \int_{f(b)}^{f(a)} f^{-1}(t) d t$
but also, $A = bf(a) - af(a) \int_a^b f(x) d x$
so $$bf(a) - bf(b) - \int_{f(b)}^{f(a)} f^{-1}(t) d = bf(a) - af(a) \int_a^b f(x) d x$$ $$\int_a^b f(x) d x = bf(a) - af(a) - \left[bf(a) - bf(b) - \int_{f(b)}^{f(a)} f^{-1}(t) d t\right]$$ $$\int_a^b f(x) d x = bf(b) - af(a) + \int_{f(b)}^{f(a)} f^{-1}(t) d t $$
The difference with the first formula is that $\int_{f(b)}^{f(a)} f^{-1}(t) d t$ is added, not subtracted. Additionally, the boundaries are swapped, as $f(b)$ is less than $f(a)$.
First, we can find the value of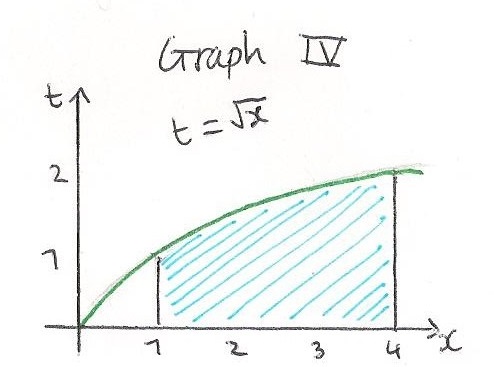 $\int_1^4\sqrt t dt$ the conventional
$\int_1^4\sqrt t dt$ the conventional
way:
$$\eqalign{\int_1^4 \sqrt x dx &= \left[\frac23 x^\frac32\right]_1^4 \\
&= \frac23 ( 4^\frac32 - 1^\frac32) \\
&= \frac{14}3}$$
Now using our formula:
$$\eqalign{\int_1^4 \sqrt x dx &= bf(b) - af(a) - \int_{f(a)}^{f(b)}f^{-1}(t)dt \\
&= 4\sqrt4 - 1\sqrt1 - \int_{\sqrt(1)}^{\sqrt(4)} t^2 dt \\
&= 8 - 1 - \left[\frac13 t^3 \right]_1^2 \\
&= 7 - \frac83 + \frac13 \\
&= \frac{14}3}$$
Which gives the same answer!
For $\sin^{-1}(x)$, using Graph V: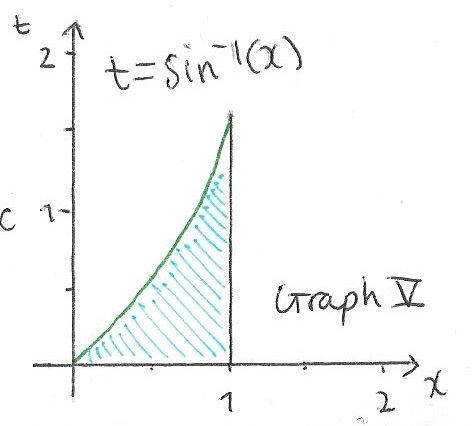
$$ \eqalign{ \int_0^1 \sin^{-1}(x) dx &= bf(b) - af(a) - \int_{f(a)}^{f(b)}f^{-1}(t)dt \\ &= 1\times \sin^{-1}(1) - 0\times \sin^{-1}(0) - \int_{f(a)}^{f(b)} \sin(t) dt \\ &= \frac{\pi}2 - 0 - \int_0^{\frac{\pi}2} \sin(t) dt \\ &=\frac{\pi}2 - \left[-\cos(t)\right]_0^{\frac{\pi}2} \\ &= \frac{\pi}2 - \left[(-cos(\frac{\pi}2)-(-cos(0))\right]\\ &= \frac{\pi}2 - 1}$$
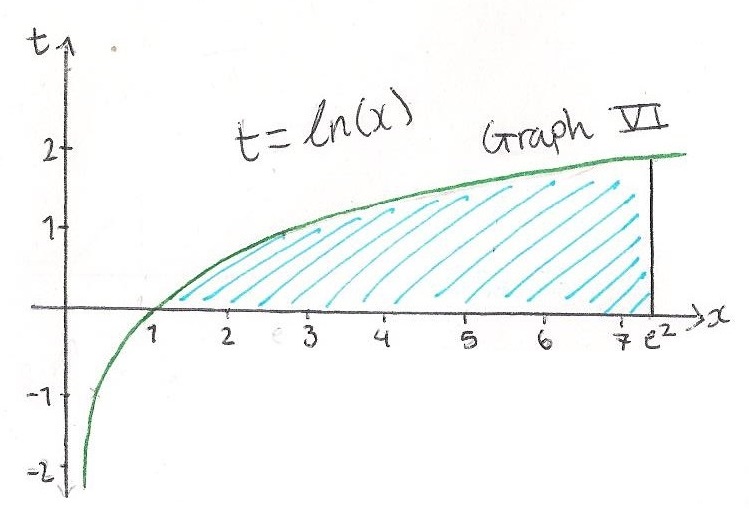
Another function that can be integrated using this method is $ln(x)$:
$$ \eqalign{\int_1^{e^2} ln(x) dx &= e^2ln(e^2) - 1ln(1) - \int_0^2 e^t dt \\ &= 2e^2 - 0 - \left[e^t\right]_0^2 \\ &= 2e^2 - (e^2 - e^0) \\
&= 2e^2 - e^2 + 1 \\ &= e^2 + 1}$$

As you can see in Graph I, the areas in purple and blue add up to the big rectangle, $bf(b)$, minus $af(a)$, the small rectangle.
There is a change of variable in $f^{-1}(t)$ because the area isn't taken
from the x-axis, but from the t-axis. $f^{-1}(x)$ is the inverse of $f(x)$. It is obtained either by switching variables and rearranging the equation again or by reflecting it in the line y=x.

The reason why $f(x)$ must be increasing in the interval $a \leq x \leq b$ is shown in Graph II. If it weren't, if at some point it reached a turning point and began to decrease, the area (orange) at the top would not be accounted for.

If $f(x)$ is always decreasing in the interval $a \leq x \leq b$, a similar formula comes out, but through more algebraic manipulation. The area called A in Graph III is:
$A = bf(a) - bf(b) - \int_{f(b)}^{f(a)} f^{-1}(t) d t$
but also, $A = bf(a) - af(a) \int_a^b f(x) d x$
so $$bf(a) - bf(b) - \int_{f(b)}^{f(a)} f^{-1}(t) d = bf(a) - af(a) \int_a^b f(x) d x$$ $$\int_a^b f(x) d x = bf(a) - af(a) - \left[bf(a) - bf(b) - \int_{f(b)}^{f(a)} f^{-1}(t) d t\right]$$ $$\int_a^b f(x) d x = bf(b) - af(a) + \int_{f(b)}^{f(a)} f^{-1}(t) d t $$
The difference with the first formula is that $\int_{f(b)}^{f(a)} f^{-1}(t) d t$ is added, not subtracted. Additionally, the boundaries are swapped, as $f(b)$ is less than $f(a)$.
First, we can find the value of
 $\int_1^4\sqrt t dt$ the conventional
$\int_1^4\sqrt t dt$ the conventionalway:
$$\eqalign{\int_1^4 \sqrt x dx &= \left[\frac23 x^\frac32\right]_1^4 \\
&= \frac23 ( 4^\frac32 - 1^\frac32) \\
&= \frac{14}3}$$
Now using our formula:
$$\eqalign{\int_1^4 \sqrt x dx &= bf(b) - af(a) - \int_{f(a)}^{f(b)}f^{-1}(t)dt \\
&= 4\sqrt4 - 1\sqrt1 - \int_{\sqrt(1)}^{\sqrt(4)} t^2 dt \\
&= 8 - 1 - \left[\frac13 t^3 \right]_1^2 \\
&= 7 - \frac83 + \frac13 \\
&= \frac{14}3}$$
Which gives the same answer!
For $\sin^{-1}(x)$, using Graph V:

$$ \eqalign{ \int_0^1 \sin^{-1}(x) dx &= bf(b) - af(a) - \int_{f(a)}^{f(b)}f^{-1}(t)dt \\ &= 1\times \sin^{-1}(1) - 0\times \sin^{-1}(0) - \int_{f(a)}^{f(b)} \sin(t) dt \\ &= \frac{\pi}2 - 0 - \int_0^{\frac{\pi}2} \sin(t) dt \\ &=\frac{\pi}2 - \left[-\cos(t)\right]_0^{\frac{\pi}2} \\ &= \frac{\pi}2 - \left[(-cos(\frac{\pi}2)-(-cos(0))\right]\\ &= \frac{\pi}2 - 1}$$

Another function that can be integrated using this method is $ln(x)$:
$$ \eqalign{\int_1^{e^2} ln(x) dx &= e^2ln(e^2) - 1ln(1) - \int_0^2 e^t dt \\ &= 2e^2 - 0 - \left[e^t\right]_0^2 \\ &= 2e^2 - (e^2 - e^0) \\
&= 2e^2 - e^2 + 1 \\ &= e^2 + 1}$$

