On the Edge

On the Edge printable sheet
 

Here are four tiles:

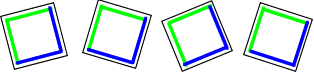
They can be arranged in a $2$ by $2$ square so that this large square has a green edge:

If the tiles are moved around, we can make a $2$ by $2$ square with a blue edge:

If I had nine tiles it would be quite easy to paint them so that, when they were arranged in a $3$ by $3$ square, the edge of this large square is green. I would need four tiles for the corners of the square, four tiles for the edges and one tile would go in the middle of the square so wouldn't need painting at all.

This is how the green-edged square would be made:

But I also want to be able to make a square with a blue edge and another square with a yellow edge.

How can the other sides of these tiles be painted so that all nine tiles can be rearranged to make two more $3$ by $3$ squares - one with a blue edge and one with a yellow edge?

Now try to colour sixteen tiles so that four $4$ by $4$ squares can be made - one with a green edge, one with a blue edge, one with a yellow edge and one with a red edge.

Find a way to colour $25$ tiles so that five $5$ by $5$ squares can be made, each with a differently coloured edge.

Do you think this is possible for $36$ tiles and six coloured edges?

Will it always be possible to add an extra colour as the squares get larger?

For a 3D version of this problem why not try " Inside Out "?

Click here for a poster of this problem.