Timber!
At the edge of the playground in our school, there is a tall tree.
Unfortunately, the tree has a disease and so the caretaker would like it cut down before it falls down.
The caretaker would like to find out whether it is safe to cut the tree at the base of its trunk. Everyone wants to be very sure that the tree will not damage the school as it falls.
How might the caretaker estimate the height of the tree and therefore work out whether the school buildings are safe?
Talk to someone else about your ideas, then click below to see what two other children suggest.
We can wait for a sunny day!
We can then measure the distance from the tree to the school buildings, and we can measure the length of the shadow of the tree.
If we push a cane into the ground so that exactly 1 metre sticks out, we can measure the shadow of the cane too.
We'll then be able to work out the height of the tree!
Will Mo's method work? How do you know?
How would you use the measurements to find out the height of the tree?
Our teacher can bend over and look through their legs!
They need to walk far enough from the tree to a find a place where they are just able to see the top of the tree (from their upside-down position).
The distance from this place to the base of the tree will be the height of the tree, approximately.
Will Sam's method work? How do you know?
Click below to see a picture which might help you think about Sam's suggestion.
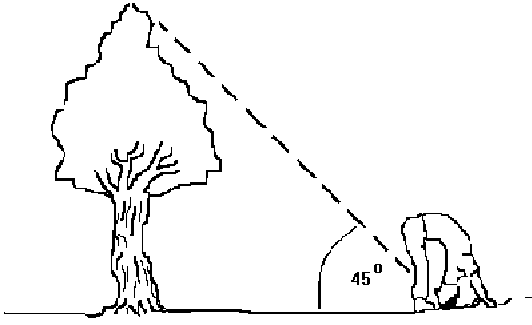
You might like to try out these two methods for yourself with you class.
If you and some friends try Mo's method, and your teacher tries Sam's method for the same tree, do you get similar answers?
We would love to hear your thoughts about Mo's and Sam's methods, and your own experiments!
You may also like
Pumpkin Pie Problem
Peter wanted to make two pies for a party. His mother had a recipe for him to use. However, she always made 80 pies at a time. Did Peter have enough ingredients to make two pumpkin pies?
Cherry Buns
Sam's grandmother has an old recipe for cherry buns. She has enough mixture to put 45 grams in each of 12 paper cake cases. What was the weight of one egg?
Orange Drink
A 750 ml bottle of concentrated orange squash is enough to make fifteen 250 ml glasses of diluted orange drink. How much water is needed to make 10 litres of this drink?