Timber!
Timber!
At the edge of the playground in our school, there is a tall tree.
Unfortunately, the tree has a disease and so the caretaker would like it cut down before it falls down.
The caretaker would like to find out whether it is safe to cut the tree at the base of its trunk. Everyone wants to be very sure that the tree will not damage the school as it falls.
How might the caretaker estimate the height of the tree and therefore work out whether the school buildings are safe?
Talk to someone else about your ideas, then click below to see what two other children suggest.
We can wait for a sunny day!
We can then measure the distance from the tree to the school buildings, and we can measure the length of the shadow of the tree.
If we push a cane into the ground so that exactly 1 metre sticks out, we can measure the shadow of the cane too.
We'll then be able to work out the height of the tree!
Will Mo's method work? How do you know?
How would you use the measurements to find out the height of the tree?
Our teacher can bend over and look through their legs!
They need to walk far enough from the tree to a find a place where they are just able to see the top of the tree (from their upside-down position).
The distance from this place to the base of the tree will be the height of the tree, approximately.
Will Sam's method work? How do you know?
Click below to see a picture which might help you think about Sam's suggestion.
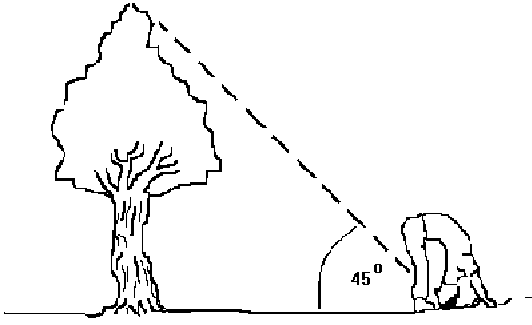
You might like to try out these two methods for yourself with you class.
If you and some friends try Mo's method, and your teacher tries Sam's method for the same tree, do you get similar answers?
We would love to hear your thoughts about Mo's and Sam's methods, and your own experiments!
Why do this problem?
This problem offers an intriguing context which learners can explore for themselves practically. As they consider why each method works, they will be drawing on their knowledge of fractions and ratio, and angles in a triangle.
Possible approach
This problem featured in the NRICH Primary webinar in April 2022.
You may choose to introduce this task outside, using a tree in your own school environment as the context rather than the fictional context in the problem as written.
Whatever context you choose, once you have posed the challenge of needing to find out the height of the tree, give learners time to talk in pairs about what they could do. You may find that some children suggest Mo's and/or Sam's method themselves, in which case you won't need to introduce the characters of Mo/Sam.
The main point of this task is to give pupils the opportunity to consider why these two methods work, so give pairs plenty of time to think together. Encourage them to use whatever resources they wish to help them in their task. As they talk, wander round the room and listen out for those who are making progress. Bringing everyone together for a mini plenary will give the class chance to hear about others' ideas. This benefits those who feel stuck, but also helps those who have made progress to clarify their ideas as they explain their thinking to others.
If appropriate, you could reveal the picture that accompanies Sam's method on screen. You could warn the class when you're about to show it, so that individuals can choose whether or not to look. Can learners use this picture to sketch a triangle that might help them think about Sam's method? You may wish to print out copies of this sheet for learners, which gives Sam's method and the picture.
In the final plenary, invite a few pairs of children to outline their reasoning for each method. Encourage the rest of the class to ask questions for clarification and facilitate a discussion so that a consensus is reached.
A lovely way to follow up this task would be to try both methods out in your own school grounds, if possible. Do the two methods give similar answers?
Key questions
Have you tried drawing a picture or diagram of each method?
In Mo's method, what is the relationship between the length of the cane and the length of its shadow? How could that help you work out the height of the tree if you know the length of the tree's shadow?
How might the picture of Sam's method included in the problem help?
Possible extension
You could invite learners to find out about other ways of estimating the height of a tree. The two methods outlined in this task have been chosen deliberately as they can be explained using mathematics usually encountered by upper primary learners. Some of the new ways they find out about might use knowledge and skills that they have not met yet, but that does not necessarily matter. It can be motivating to know that in a few years' time, they will be equipped with the understanding needed to explain why another method works.
Possible support
Drawing a diagram or picture is a good way to get started on this task. Some learners might find it helpful to work with real numbers in order to unpick Mo's method. In this case, the following examples might help:
Length of tree's shadow: 36.3m
Length of cane's shadow: 1.23m
You may also like
Pumpkin Pie Problem
Peter wanted to make two pies for a party. His mother had a recipe for him to use. However, she always made 80 pies at a time. Did Peter have enough ingredients to make two pumpkin pies?
Cherry Buns
Sam's grandmother has an old recipe for cherry buns. She has enough mixture to put 45 grams in each of 12 paper cake cases. What was the weight of one egg?
Orange Drink
A 750 ml bottle of concentrated orange squash is enough to make fifteen 250 ml glasses of diluted orange drink. How much water is needed to make 10 litres of this drink?