A-maze-ing

Did you know that ancient traditional mazes often tell a story? One such story is ancient Celtic tale The Raid of Fraech's Cattle. The story tells how the hero Conall Cernach helps to rescue Fraech's magic cows which have been stolen by some warriors. The valuable cows are being kept with other treasures inside a mountain fortress, guarded by a mighty serpent. A helpful milk maid lets Conall into the fortress at night. It appears that the hero and the serpent may have met before because, instead of attacking Conall, the snake darts into his waist belt. After releasing the cows and taking some treasure, Conall lets the snake out of his belt without harming it and leaves the fortress.
 

Remembering this story helps to draw the basic maze pattern: The fortress of the mighty serpent of Val Camonica. To draw it, you will need a pencil and an eraser.

First draw the stick figure for Conall, wearing his horned hat. Then draw a spiral, starting over his head, through his middle, around twice, stopping just before his legs, and close off the spiral. This is the long serpent passing through his waist belt. (Don't draw the coils of the snake too close together).
 

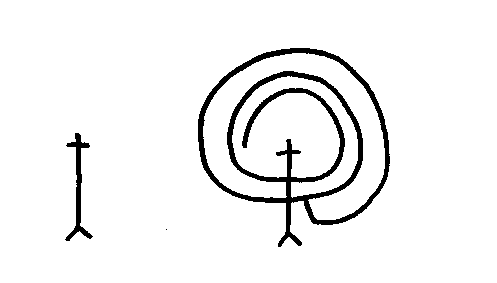
Now erase a the bottom piece of the snake that crosses the figure, and erase the legs. (Conall slips the snake out of his belt and leaves the fortress).
 

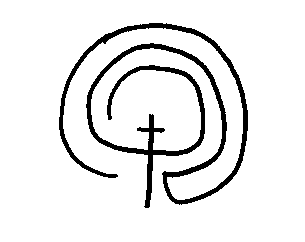
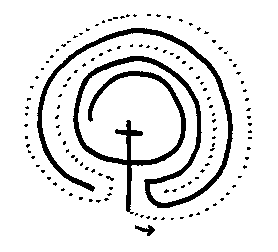
Just two inside walls to draw now. First, start at the beginning of the snake. Go down then up and over the top of the hat. Start a new line at the very top of the hat. Go down then, up over the line you just drew. Carefully erase the horns from the hat and the fortress is complete.

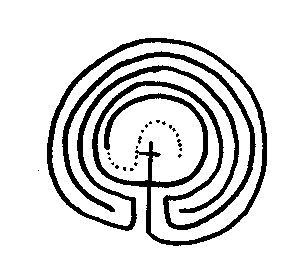
This is a traditional Camonica Valley Maze. This and other mazes can be found in the book Celtic Design: Maze Patterns by Aidan Meehan.

For more about mazes why not look at the " More on Mazes " article.