The Konigsberg Bridge Problem
This article has now been replaced by the problem The Bridges of Konigsberg.
Konigsberg is a town on the Preger River, which in the 18th century was a German town, but now is Russian. Within the town are two river islands that are connected to the banks with seven bridges (as shown below).
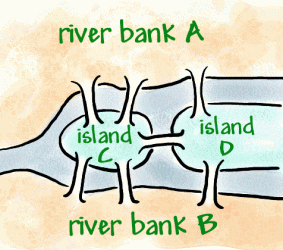
It became a tradition to try to walk around the town in a way that only crossed each bridge once, but it proved to be a difficult problem. Leonhard Euler, a Swiss mathematician in the service of the Russian empress Catherine the Great, heard about the problem. In 1736 Euler proved that the walk was not possible to do. He proved this by inventing a kind of diagram called a network, that is made up
of vertices (dots where lines meet) and arcs (lines).
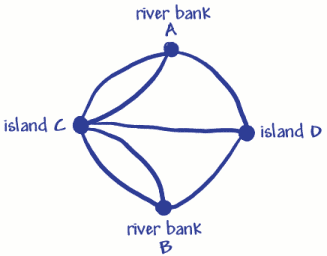
He used four dots (vertices) for the two riverbanks and the two islands. These have been marked A, B and C, D. The seven lines (arcs) are the seven bridges. You can see that 3 bridges (arcs) join to riverbank A, and 3 join to riverbank B. 5 bridges (arcs) join to island C, and 3 join to island D. This means that all the vertices have an odd number of arcs, so they are called odd vertices. (An
even vertex would have to have an even number of arcs joining to it).
Remember that the problem was to travel around town crossing each bridge only once. On Euler's network this meant tracing over each arc only once, visiting all the vertices. Euler proved it couldn't be done because he worked out that to have an odd vertex you would have to begin or end the trip at that vertex. (Think about it). Since there can only be one beginning and one end, there can only be
two odd vertices if you're going to be able to trace over each arc only once. Since the bridge problem has 4 odd vertices, it just isn't possible to do! What happens if there are no odd vertices at all? Can this network be traced?
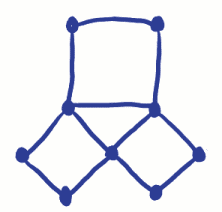
The invention of networks began a whole new type of geometry called Topology. Topology is now used in many ways, including for planning and mapping railway networks. (Ahhh! Trains had to come into it....)
You may also like
Icosian Game
This problem is about investigating whether it is possible to start at one vertex of a platonic solid and visit every other vertex once only returning to the vertex you started at.
Königsberg
Can you cross each of the seven bridges that join the north and south of the river to the two islands, once and once only, without retracing your steps?
Travelling Salesman
A Hamiltonian circuit is a continuous path in a graph that passes through each of the vertices exactly once and returns to the start. How many Hamiltonian circuits can you find in these graphs?