Skip over navigation
In February 1999, we had the story of an ancient Celtic maze . There is a long tradition of creating mazes throughout history and across the world. Some mazes told stories, some had religious meaning, some were for defence against invaders and some were made as outdoor amusements for rich people. There are now many public mazes where people can enjoy the challenge of trying to find their way through the maze.
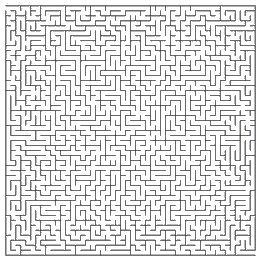
The most common mazes we see are those drawn on paper as puzzles. You can eventually solve a maze by just trying all the paths until you get lucky, but you think about what you are doing you can become quite clever at finding the way quickly. Some mazes are drawn very carefully using a traditional method or a mathematical pattern. If you'd like to find out more about this, visit the Through Mazes to Mathematics website.
Lewis Carroll (famous for writing Alice in Wonderland) was a mathematician. When he was in his twenties he drew a very tricky maze with paths that crossed under and over each other. The Year 7 Maths Club from Bexley Grammar School suggested this maze a challenge. If you click here on Lewis Carroll's Maze , you will go to a page that can be printed off. Challenge your friends to find a way from the middle to the outside before you do!
More on Mazes
In February 1999, we had the story of an ancient Celtic maze . There is a long tradition of creating mazes throughout history and across the world. Some mazes told stories, some had religious meaning, some were for defence against invaders and some were made as outdoor amusements for rich people. There are now many public mazes where people can enjoy the challenge of trying to find their way through the maze.
If you like looking at mazes, there's an excellent English
website (http://www.mazemaker.com/) that
has pictures of many different types of mazes that can be visited.
For example; the hedge mazes at Leeds Castle or Edinburgh Zoo; or
the mirror maze at Wookey Hole Caves; or the stone path maze in
Bath. The man who created this website is a maze designer and so
has collected a huge range of mazes. There are databases of 'Mazes
of the World', cornfield mazes and 'Mazes in Outer Space'. If you'd
like to try doing a maze puzzle, try 'Queen's Maze', or 'Tumbling
Log Maze (As always - never make contact with anyone over the
internet without asking your parents).
The most common mazes we see are those drawn on paper as puzzles. You can eventually solve a maze by just trying all the paths until you get lucky, but you think about what you are doing you can become quite clever at finding the way quickly. Some mazes are drawn very carefully using a traditional method or a mathematical pattern. If you'd like to find out more about this, visit the Through Mazes to Mathematics website.
Lewis Carroll (famous for writing Alice in Wonderland) was a mathematician. When he was in his twenties he drew a very tricky maze with paths that crossed under and over each other. The Year 7 Maths Club from Bexley Grammar School suggested this maze a challenge. If you click here on Lewis Carroll's Maze , you will go to a page that can be printed off. Challenge your friends to find a way from the middle to the outside before you do!
You may also like
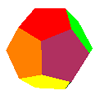
Icosian Game
This problem is about investigating whether it is possible to start at one vertex of a platonic solid and visit every other vertex once only returning to the vertex you started at.
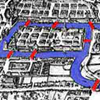
Königsberg
Can you cross each of the seven bridges that join the north and south of the river to the two islands, once and once only, without retracing your steps?
Travelling Salesman
A Hamiltonian circuit is a continuous path in a graph that passes through each of the vertices exactly once and returns to the start. How many Hamiltonian circuits can you find in these graphs?