Skip over navigation
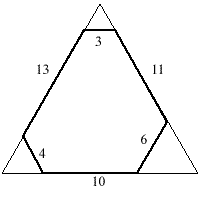
The diagram shows an irregular hexagon with interior angles all equal to 120 degrees made by cutting the corners off a piece of card in the shape of an equilateral triangle with sides of length 20 units.
An identical hexagon could also be made by cutting the corners off a different equilateral triangle.
What is the side length of this triangle?
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Hexagon Cut Out
Age 11 to 14
ShortChallenge Level 
The diagram shows an irregular hexagon with interior angles all equal to 120 degrees made by cutting the corners off a piece of card in the shape of an equilateral triangle with sides of length 20 units.
An identical hexagon could also be made by cutting the corners off a different equilateral triangle.
What is the side length of this triangle?
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Cube Paths
Given a 2 by 2 by 2 skeletal cube with one route `down' the cube. How many routes are there from A to B?
Coins on a Plate
Points A, B and C are the centres of three circles, each one of which touches the other two. Prove that the perimeter of the triangle ABC is equal to the diameter of the largest circle.