Skip over navigation
The other triangle has side length 27.
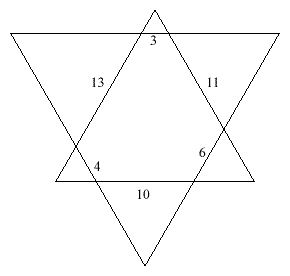
By extending the short sides, one can construct another triangle. Since all the angles involved are 60 degrees, the new small triangles and the new large triangle are all equilateral. The sides of the new, large triangle are:
Hexagon Cut Out
Age 11 to 14
ShortChallenge Level 
The other triangle has side length 27.
By extending the short sides, one can construct another triangle. Since all the angles involved are 60 degrees, the new small triangles and the new large triangle are all equilateral. The sides of the new, large triangle are:
13 + 3 + 11 = 11 + 6 + 10 = 10 + 4 + 13 = 27
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Cube Paths
Given a 2 by 2 by 2 skeletal cube with one route `down' the cube. How many routes are there from A to B?
Coins on a Plate
Points A, B and C are the centres of three circles, each one of which touches the other two. Prove that the perimeter of the triangle ABC is equal to the diameter of the largest circle.