Skip over navigation
The graph below is a coordinate system based on $60$ $^\circ$ angles. It was drawn on isometric paper.
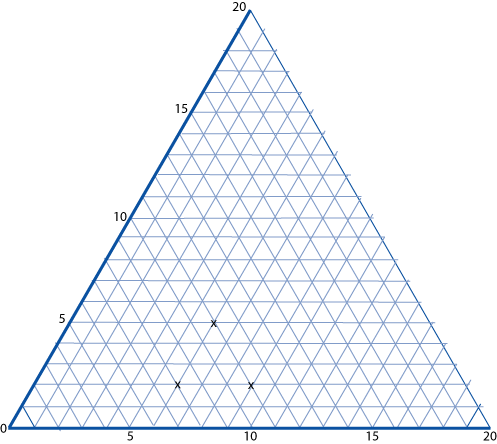
The marked points are $(6, 2)$, $(6, 5)$ and $(9, 2)$. When joined they form an equilateral triangle.
The following five sets of points are also triangles.
A. $(1, 13), (6, 8)$ and $(6, 13)$.
B. $(1, 1), (3, 3)$ and $(7, 1)$.
C. $(12, 1), (17, 1)$ and $(8, 9)$.
D. $(1, 10), (5, 2)$ and $(6, 6)$.
E. $(7, 5), (15, 4)$ and $(7, 11)$.
What kinds of triangles are they?
Can you work out any of the angles at the vertices?
Cartesian Isometric
Age 7 to 11
Challenge Level 
Cartesian Isometric
The graph below is a coordinate system based on $60$ $^\circ$ angles. It was drawn on isometric paper.
The marked points are $(6, 2)$, $(6, 5)$ and $(9, 2)$. When joined they form an equilateral triangle.
The following five sets of points are also triangles.
A. $(1, 13), (6, 8)$ and $(6, 13)$.
B. $(1, 1), (3, 3)$ and $(7, 1)$.
C. $(12, 1), (17, 1)$ and $(8, 9)$.
D. $(1, 10), (5, 2)$ and $(6, 6)$.
E. $(7, 5), (15, 4)$ and $(7, 11)$.
What kinds of triangles are they?
Can you work out any of the angles at the vertices?
Why do this problem?
This problem has an unusual context for coordinates which will provide an extra challenge when the group are working on coordinates or the angle properties of shapes.
Pupils need to be encouraged to look very carefully at the angles of the triangles. Isometric paper is almost essential.
Key questions
Do you think it would help to draw the triangle out on isometric paper?
What are the angles created in the small triangles on the paper?When you're were working out the angles in the triangles did you notice how the sides cut through the grid triangles?
Possible extension
Learners could make their own graph on isometric paper.
Possible support
Suggest doing a less unusual and less difficult problem on coordinates such as Two Number Lines.You may also like
Timber!
How can the school caretaker be sure that the tree would miss the school buildings if it fell?
Fred the Class Robot
Billy's class had a robot called Fred who could draw with chalk held underneath him. What shapes did the pupils make Fred draw?