Fence It

Why do this problem?

This problem challenges students to work systematically while applying their knowledge of areas of rectangles. It offers opportunities for higher level mathematical thinking (optimising and graphing) in a context that doesn't require sophisticated mathematical content.
This problem could be revisited when students are older and are able to use algebraic techniques (forming quadratic expressions, maximising by completing the square).

Possible approach

This printable worksheet may be useful: Fence It.

"Imagine you had $40$ one-metre sections of fencing, and you wanted to make a rectangular enclosure. On your whiteboards, sketch a possible rectangle you could make that uses all $40$m. Write the area of your rectangle inside."

Tabulate students' responses on the board. Select the largest area that has been found so far: "Is this the largest possible area we can make with $40$m of fencing?" Once the $10$m square with area $100$m$^2$ has been found, "How can we be convinced that a larger area isn't possible?" Give students a few minutes to think about the question in pairs and develop some convincing arguments. Circulate and listen in on conversations to identify which pairs have something worth sharing. Look out for diagram representations similar to this one:



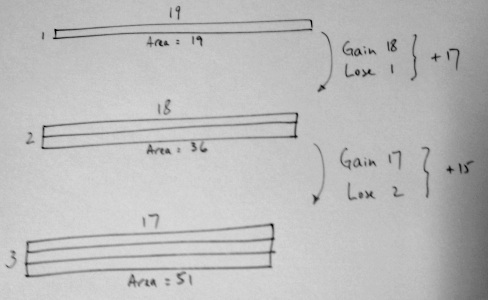
or tables of values like this one:



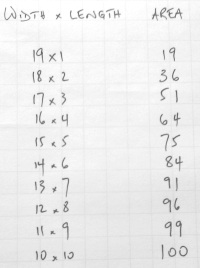
Bring the class back together and invite any pairs whose interesting insights you noticed to share their thoughts. Use this to write an agreed 'convincing argument' why a square gives the maximum area, modelling the level of rigour that you expect them to come up with in their own justifications later on.

Now set the second problem: "Imagine you had a long wall that you could use as one of the sides of your enclosure, so your $40$ metres of fencing only has to go round three sides of the rectangle. Use the ideas we have shared to work with your partner and find the biggest possible enclosure now. Make sure you have a justification to convince everyone that your area is the biggest possible."

This worksheet has all three parts of the problem on, so you could hand this out to students who finish the second task quickly.

Before the end of the lesson, allow some time for students to present their findings, focussing particularly on their justifications.

Key questions

What would the width of the rectangle be if the length is 1m? 2m? 3m? ...
How can I be sure I have found the maximum possible area?

Possible support

Share the diagrams above to help students to represent their trial-and-improvement strategies in a clear way that shows how the area changes.

Possible extension

Some students may use algebra to represent the scenarios and use graphical methods to find/justify the optimal solution.

Relaxing the straight lines constraint would allow students to consider some circle geometry:
"Could you enclose even greater areas if you had 40m of flexible wire fencing that could fence off curves as well as straight lines?"