Fence It

There are many ways to solve this one, and we received a lot of great anwsers. Since the questions appear to get harder and harder, let's start with the first problem.

What is the largest rectangular area of land you could fence off with 40m of fencing?

Amy tried lots of different possible side lengths for the rectangle. She used the base times height formula to get the area.

base (m)	height (m)	area (m2)
10	10	100
9	11	99
5	15	75
1	19	19

From this I think that the answer is 100m² because the table shows the less
gap between the two numbers the larger the area and there isn't a gap
between 10 and 10 so it must be them.

This reasoning sounds right, well done. Don't worry that with a base and height of 10m the area fenced off makes a square; a square is just a special kind of rectangle! If we do a bit more thinking can we be absolutely certain there isn't some way of improving on 100m²? Nathan used the letters x and y to represent the  base and the height of the rectangle.

If the sides are length x and y metres, then the perimeter of the rectangle is 2x+2y metres. Since this is all the fence we can use we must have 2x+2y=40. The area of the rectangle is x times y which I can write as xy.

From the first equation we know that 2y=40-2x so that y=20-x.
Then the formula for the area can be written
xy = x(20-x) = 20x-x².

The largest value the expression 20x-x² can take is 100, which is when x=10.

This is exactly right. If you draw a graph of the function 20x-x² you'll see that it is highest at x=10, with a value of 200. There are also advanced techniques which can help find the highest point if you can't draw a graph.

A really special symmetry argument goes like this: in the equations 2x+2y=40 and Area=xy, there is nothing different between x and y; you could swap their names and the equations would be the same. This often means that the values of x and y should be the same.

What is the largest rectangular area you can fence off with a wall for one side?

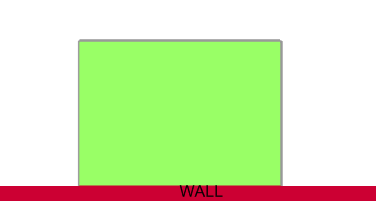
Braiden noticed the following, and made a list of possible solutions.

The second question gives you the same amount of fence sections but only three sides of a rectangle need to be filled.
 

With trial and improvement he found that a 10 by 20 rectangle was the best. Well done. Can you see how the algebraic method with x and y might be used for this question too? We can say that the side opposite the wall is length x, and the other two fenced sides are length y.

The formula for the amount of fence used in the perimeter is x+2y=40.
The area is xy like before.
Notice x = 40-2y so we get:
Area = xy = (40-2y)y = 40y-2y².

Now draw a graph or use advanced techniques to find the highest point of this function: 40y-y². At y=10 we get an area of 200m². Notice that in this case x=20, so the fenced area isn't a square.

What is the largest area you can fence off with the attachment point marked?

This third problem is the hardest, but both trial and improvement and algebra can help us find the answer. Kaedan noticed that you can split the area into smaller rectangles. The picture below might help too.


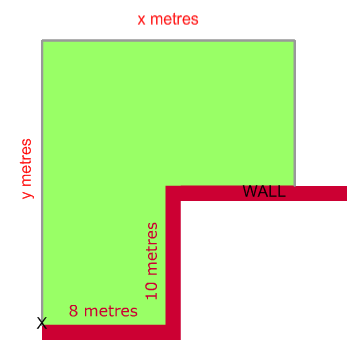
With the sides labelled what is the area covered? And what is the length of fence used? A few people managed to work this one out, well done!

First the area. We have 8x10=80m² in the lower left corner.
The remaining rectangle has base x metres long, and height y-10.
Then the total area is 80+x(y-10).
This can be written Area = 80+xy-10x.

Now the perimeter. We use y+x+y-10 metres of fence. That is x+2y-10=40.

Some people made a table of values to work out the last bit, and the algebra works too.

The perimeter equation mean that x=50-2y, so the area equation is
Area = 80+50y-2y²-500+20y = 70y-2y²-420.
By plotting a graph or using another method we can see that the largest value is found at y=17.5. This makes an area of 192.5m².

Extension: what about curved fences?

There are so many different shapes with curved sides, and you might not know a formula for the area for each one. Try a few shapes that you do know the area of and see what you can come up with. Can you beat the best values we found with rectangles and straight sides? Do you need different shapes or will one always win?