Skip over navigation
Congratulations to Curt, Reigate College and to Andrei, Tudor Vianu National College, Bucharest, Romania for you solutions to this problem
When AB is a diameter angle $ACB$ is 90 degrees so we can use Pythagoras' Theorem. The area of the triangle is given by $\textstyle{1\over 2}ab = \textstyle {1\over 2}ch$ where $h$ is the length of the perpendicular from $C$ to $AB$. Then
$$(a+b)^2=a^2+b^2+2ab=c^2+2ch.$$
Thus $(a+b)^2$ is a maximum when $h$ is a maximum and equal to the radius of the circle $\textstyle {1\over 2}c$ . So the maximum value of $a+b$ is $c\sqrt 2$.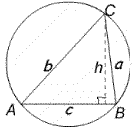
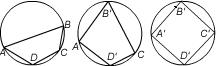Labelling $Q$ as $ABCD$, consider triangle $ABC$ with $AC$ fixed
and $B$ varying. Let $B'$ be the position of $B$ when, by the
previous result $AB + BC$ is a maximum, that is when $AB = BC$ Note
that this also gives the maximum area of triangle $ABC$. Similarly
by considering triangle $ADC$ with $AC$ fixed, we find $D'$ where
$AD+DC$ is a maximum and $AD=DC$. Now $B'D'$ is a diameter, keep
this fixed and consider triangles $B'CD'$ and $B'AD'$. The
positions of $C$ and $A$ that maximise the perimeter and area are
$C'$ and $A'$ where $A'C'$ is a diameter. Hence, for the perimeter
and area of $Q$ to be a maximum all the sides of the quadrilateral
must be equal making $Q$ a square. Hence the maximum perimeter is
$4r\sqrt 2$ and the maximum area is $2r^2$.
Cyclic Triangles
Age 16 to 18
Challenge Level 
Congratulations to Curt, Reigate College and to Andrei, Tudor Vianu National College, Bucharest, Romania for you solutions to this problem
When AB is a diameter angle $ACB$ is 90 degrees so we can use Pythagoras' Theorem. The area of the triangle is given by $\textstyle{1\over 2}ab = \textstyle {1\over 2}ch$ where $h$ is the length of the perpendicular from $C$ to $AB$. Then
$$(a+b)^2=a^2+b^2+2ab=c^2+2ch.$$
Thus $(a+b)^2$ is a maximum when $h$ is a maximum and equal to the radius of the circle $\textstyle {1\over 2}c$ . So the maximum value of $a+b$ is $c\sqrt 2$.
When $AB$ is not a diameter we have (using the Cosine
Rule):
$$\eqalign{ (a+b)^2 &= a^2 +b^2 + 2ab \cr &= c^2 +
2ab\cos \angle ACB +2ab \cr &= c^2 +2ab(1+\cos \angle ACB) \cr
&=c^2 +4ab \cos^2 \textstyle {1\over 2}\angle ACB.}.$$
As the area of triangle $ACB$ is given by $\Delta = \textstyle
{1\over 2} ab\sin \angle ACB$ we have
$$\eqalign { (a+b)^2 &= c^2 + {8\Delta \cos^2
\textstyle{1\over 2}\angle ACB \over \sin\angle ACB} \cr &= c^2
+ 4\Delta \cot \textstyle {1\over 2}\angle ACB }.$$
If we keep $A$ and $B$ fixed and vary $C$ then, as $c$ and
$\angle ACB$ are constant, and the area of the triangle $\Delta$ is
a maximum when $h$ is a maximum, it follows that $a + b$ is a
maximum when $h$ is a maximum, that is when $a=b$ and the altitude
of the triangle drawn from $C$ to $AB$ is a line of symmetry of the
triangle. In this case
$$a=b={c\over 2\sin \textstyle {1\over 2}\angle ACB}.$$
Conjecture: Let $Q$ be a variable cyclic quadrilateral in a
circle of radius $r$. Then the area and the perimeter of $Q$ will
be a maximum when $Q$ is a square; that is when each of the
diagonals of the quadrilateral is a diameter and each diagonal
bisects of the other diagonal at right angles.
You may also like
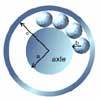
Ball Bearings
If a is the radius of the axle, b the radius of each ball-bearing, and c the radius of the hub, why does the number of ball bearings n determine the ratio c/a? Find a formula for c/a in terms of n.
Overarch 2
Bricks are 20cm long and 10cm high. How high could an arch be built without mortar on a flat horizontal surface, to overhang by 1 metre? How big an overhang is it possible to make like this?