Skip over navigation
Well done Curt from Reigate College for this solution.
If $G(x)=e^{f(x)}$, by the chain rule:
$$G'(x)=e^{f(x)} \times f'(x).$$
As $e$ is never zero, the gradient function of $G(x)$ is zero when the gradient function of $f(x)$ is zero and it always has the same sign as $f'(x)$ so $G(x)$ and $f(x)$ have the same turning points.
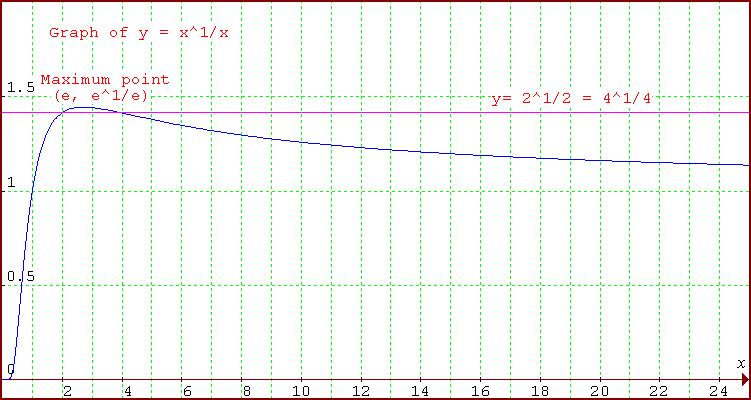
To answer the question of turning points of $G(x)=x^{1\over x}= e^{1/x\log x}$ let's first find the derivative of ${1\over x}\log x$.
$${d\over dx }f(x)={d\over dx }({1\over x}\log x) = {{1-\log x}\over x^2}.$$
The derivative is positive for $\log x < 1$, that is $x< e$, it is is zero when $\log x = 1$, $x = e$ and it is negative for $x> e$. Hence the function is increasing for $x< e$ and decreasing for $x> e$.
$${d^2\over dx^2 }({1\over x}\log x)= {{-x-2x(1-\log x)}\over x^4 }= {{2\log x -3}\over x^3}.$$
At $x=e$ the second derivative of $f(x)$ is $-1/e^3$ which is negative so $f(x)$ has a maximum and so $G(x)$ has a maximum. Therefore $(e, e^{1/e})$ is a maximum point of $G(x)=x^{1\over x}$.
To prove $\lim x^{1\over x} \rightarrow 1$ as $x\rightarrow \infty$ we may use the similar result for the discrete case $n^{1\over n}$. As the graph of $f(x)=x^{1\over x}$ is decreasing as $x\to \infty$ for each value of $x$ there is a value of $n$ for which $n^{1/n}< x^{1/x}$ and vice versa so both tend to the same limit which is $1$.
What if $x\rightarrow 0$? Well, as suggested in the question, letting $1/x=t$ in $x^{1\over x}$, one can note that as $x\rightarrow 0$, $t\rightarrow \infty$. Writing $t=1/x$, $$x^{1/x} = \left ({1\over t}\right )^t = {1\over t^t}.$$ As $x\to 0$ we have $t\to \infty$ and $t^t \to \infty$ so $$x^{1/x} = {1\over t^t} \to 0$$.
Hence the graph of $y=x^{1/x}$ is always above the line $y=0$ although the function is undefined at $x=0$.


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Exponential Trend
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Well done Curt from Reigate College for this solution.
If $G(x)=e^{f(x)}$, by the chain rule:
$$G'(x)=e^{f(x)} \times f'(x).$$
As $e$ is never zero, the gradient function of $G(x)$ is zero when the gradient function of $f(x)$ is zero and it always has the same sign as $f'(x)$ so $G(x)$ and $f(x)$ have the same turning points.
To answer the question of turning points of $G(x)=x^{1\over x}= e^{1/x\log x}$ let's first find the derivative of ${1\over x}\log x$.
$${d\over dx }f(x)={d\over dx }({1\over x}\log x) = {{1-\log x}\over x^2}.$$
The derivative is positive for $\log x < 1$, that is $x< e$, it is is zero when $\log x = 1$, $x = e$ and it is negative for $x> e$. Hence the function is increasing for $x< e$ and decreasing for $x> e$.
$${d^2\over dx^2 }({1\over x}\log x)= {{-x-2x(1-\log x)}\over x^4 }= {{2\log x -3}\over x^3}.$$
At $x=e$ the second derivative of $f(x)$ is $-1/e^3$ which is negative so $f(x)$ has a maximum and so $G(x)$ has a maximum. Therefore $(e, e^{1/e})$ is a maximum point of $G(x)=x^{1\over x}$.
To prove $\lim x^{1\over x} \rightarrow 1$ as $x\rightarrow \infty$ we may use the similar result for the discrete case $n^{1\over n}$. As the graph of $f(x)=x^{1\over x}$ is decreasing as $x\to \infty$ for each value of $x$ there is a value of $n$ for which $n^{1/n}< x^{1/x}$ and vice versa so both tend to the same limit which is $1$.
What if $x\rightarrow 0$? Well, as suggested in the question, letting $1/x=t$ in $x^{1\over x}$, one can note that as $x\rightarrow 0$, $t\rightarrow \infty$. Writing $t=1/x$, $$x^{1/x} = \left ({1\over t}\right )^t = {1\over t^t}.$$ As $x\to 0$ we have $t\to \infty$ and $t^t \to \infty$ so $$x^{1/x} = {1\over t^t} \to 0$$.
Hence the graph of $y=x^{1/x}$ is always above the line $y=0$ although the function is undefined at $x=0$.
You may also like
Folium of Descartes
Investigate the family of graphs given by the equation x^3+y^3=3axy for different values of the constant a.
Witch of Agnesi
Sketch the members of the family of graphs given by y = a^3/(x^2+a^2) for a=1, 2 and 3.

