Skip over navigation
Elizabeth from the International School of Geneva, someone from Winchester College who gave no name and Andrei from Tudor Vianu National College, Bucharest, Romania all sent solutions to this problem.
Elizabeth factorised the expression as follows:
$$\eqalign{ r^2 - r + {\textstyle{1\over 4}} \sin^2 4\theta &= 0 \cr r^2 - r + {\textstyle{1\over 4}}(2(\sin 2\theta \cos 2\theta))^2 &= 0 \cr r^2 - r + \sin^2 2\theta \cos^2 2\theta &= 0 \cr (r - \sin^2 2\theta)(r- \cos^2 2\theta) &=0.}$$
and plotted the graphs of $r = \sin^2 {2\theta}$ and $r=\cos^2 2{\theta}$.
Andrei factorised the expression differently
$$(2r+\cos {4\theta} -1)(2r \cos {4\theta} - 1)$$
and plotted the graphs of $r = \textstyle{1\over 2}(1 + \cos 4\theta)$ and $r = \textstyle{1\over 2}(1 - \cos 4\theta)$ but you should be able to see that the results are equivalent.
Our friend from Winchester College used the difference of two squares to arrive at the same form of this result as Andrei and another method would be substitution in the formula for the solution of a quadratic equation.
Consider first the graph of $r- \sin^2 2\theta=0$ in polar coordinates where $r$ is the length of the line segment from the point from the origin and $\theta$ is the angle measured counter clockwise between this line segment and the positive $x$ axis. For points on this graph, as $\theta$ increases from 0 to ${\pi \over 4}$ we have $\sin^2 2\theta$ increases from 0 to 1. Between $\theta = {\pi\over 4}$ and ${\pi \over 2}$ the value of $r$ decreases from 1 to 0 so that the graph in the first quadrant is a 'petal' symmetrical about the line $\theta = {\pi \over 4}$.
Similarly the graph in the second quadrant is a 'petal' for $\theta $ between ${\pi \over 2}$ and $\pi$ where $r$ takes positive values corresponding to $\sin^2 \theta$. The graph in the third quadrant is a 'petal' for $\theta $ between $\pi $ and ${3\pi \over 2}$ and the graph in the fourth quadrant is a 'petal' for $\theta $ between ${3\pi \over 2}$ and $2\pi$.
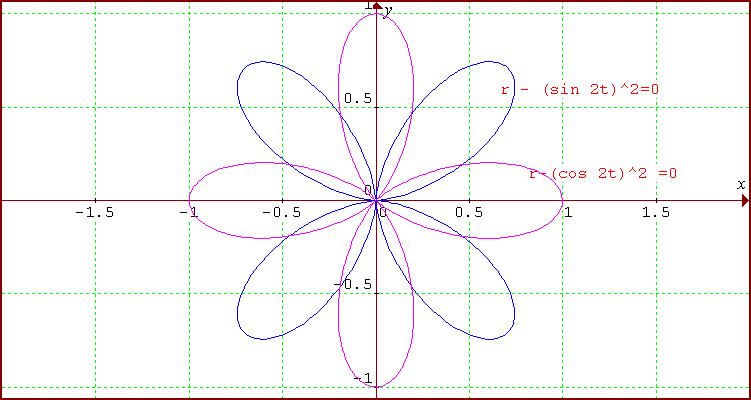
Next consider the graph of $r- \cos^2 2\theta=0$. This will be of the same form but rotated by ${\pi \over 4}$ corresponding to the phase shift between the graphs of $\sin 2\theta$ and $\cos 2\theta$.
For points on this graph, as $\theta$ increases from 0 to ${\pi \over 4}$ we have $\cos^2 2\theta$ decreases from 1 to 0. Between $\theta = {\pi\over 4}$ and ${\pi \over 2}$ the value of $r$ increases from 0 to 1 and between ${\pi \over 2}$ and ${3\pi \over 4}$, as $r$ decreases from 1 to 0, the 'petal' symmetrical about the y-axis is completed.
The next petal, symmetrical about the negative x-axis, is drawn for $\theta $ between ${3\pi \over 4}$ and ${5\pi \over 4}$. The next petal, symmetrical about the negative y-axis, is drawn for $\theta $ between ${5\pi \over 4}$ and ${7\pi \over 4}$ and the remaining petal is completed for $\theta $ between ${7\pi \over 4}$ and $2\pi$.
Polar Flower
Age 16 to 18
Challenge Level 
Elizabeth from the International School of Geneva, someone from Winchester College who gave no name and Andrei from Tudor Vianu National College, Bucharest, Romania all sent solutions to this problem.
Elizabeth factorised the expression as follows:
$$\eqalign{ r^2 - r + {\textstyle{1\over 4}} \sin^2 4\theta &= 0 \cr r^2 - r + {\textstyle{1\over 4}}(2(\sin 2\theta \cos 2\theta))^2 &= 0 \cr r^2 - r + \sin^2 2\theta \cos^2 2\theta &= 0 \cr (r - \sin^2 2\theta)(r- \cos^2 2\theta) &=0.}$$
and plotted the graphs of $r = \sin^2 {2\theta}$ and $r=\cos^2 2{\theta}$.
Andrei factorised the expression differently
$$(2r+\cos {4\theta} -1)(2r \cos {4\theta} - 1)$$
and plotted the graphs of $r = \textstyle{1\over 2}(1 + \cos 4\theta)$ and $r = \textstyle{1\over 2}(1 - \cos 4\theta)$ but you should be able to see that the results are equivalent.
Our friend from Winchester College used the difference of two squares to arrive at the same form of this result as Andrei and another method would be substitution in the formula for the solution of a quadratic equation.
Consider first the graph of $r- \sin^2 2\theta=0$ in polar coordinates where $r$ is the length of the line segment from the point from the origin and $\theta$ is the angle measured counter clockwise between this line segment and the positive $x$ axis. For points on this graph, as $\theta$ increases from 0 to ${\pi \over 4}$ we have $\sin^2 2\theta$ increases from 0 to 1. Between $\theta = {\pi\over 4}$ and ${\pi \over 2}$ the value of $r$ decreases from 1 to 0 so that the graph in the first quadrant is a 'petal' symmetrical about the line $\theta = {\pi \over 4}$.
Similarly the graph in the second quadrant is a 'petal' for $\theta $ between ${\pi \over 2}$ and $\pi$ where $r$ takes positive values corresponding to $\sin^2 \theta$. The graph in the third quadrant is a 'petal' for $\theta $ between $\pi $ and ${3\pi \over 2}$ and the graph in the fourth quadrant is a 'petal' for $\theta $ between ${3\pi \over 2}$ and $2\pi$.
Next consider the graph of $r- \cos^2 2\theta=0$. This will be of the same form but rotated by ${\pi \over 4}$ corresponding to the phase shift between the graphs of $\sin 2\theta$ and $\cos 2\theta$.
For points on this graph, as $\theta$ increases from 0 to ${\pi \over 4}$ we have $\cos^2 2\theta$ decreases from 1 to 0. Between $\theta = {\pi\over 4}$ and ${\pi \over 2}$ the value of $r$ increases from 0 to 1 and between ${\pi \over 2}$ and ${3\pi \over 4}$, as $r$ decreases from 1 to 0, the 'petal' symmetrical about the y-axis is completed.
The next petal, symmetrical about the negative x-axis, is drawn for $\theta $ between ${3\pi \over 4}$ and ${5\pi \over 4}$. The next petal, symmetrical about the negative y-axis, is drawn for $\theta $ between ${5\pi \over 4}$ and ${7\pi \over 4}$ and the remaining petal is completed for $\theta $ between ${7\pi \over 4}$ and $2\pi$.
You may also like
Maltese Cross
Sketch the graph of $xy(x^2 - y^2) = x^2 + y^2$ consisting of four curves and a single point at the origin. Convert to polar form. Describe the symmetries of the graph.
